题目内容
5．要使二次根式$\sqrt{1-x}$有意义，则x应满足（ ）| A． | x≠1 | B． | x≥1 | C． | x≤1 | D． | x＜1 |
分析 根据二次根式有意义的条件可得1-x≥0，再解即可．
解答 解：由题意得：1-x≥0，
解得：x≤1，
故选：C．
点评 此题主要考查了二次根式有意义的条件，关键是掌握二次根式中的被开方数是非负数．
练习册系列答案
相关题目
8．作为世界文化遗产的长城，其总长大约为6700000m．将6700000用科学记数法表示为（ ）
| A． | 6.7×105 | B． | 6.7×106 | C． | 0.67×107 | D． | 67×108 |
9．在《数据分析》章节测试中，“勇往直前”学习小组7位同学的成绩分别是92，88，95，93，96，95，94．这组数据的中位数和众数分别是（ ）
| A． | 94，94 | B． | 94，95 | C． | 93，95 | D． | 93，96 |
13．
有这样一个问题：探究函数y=$\frac{6}{（x-2）^{2}}$的图象与性质．
小华根据学习函数的经验，对函数y=$\frac{6}{（x-2）^{2}}$的图象与性质进行了探究．
下面是小华的探究过程，请补充完整：
（1）函数y=$\frac{6}{（x-2）^{2}}$的自变量x的取值范围是x≠2；
（2）下表是y与x的几组对应值．
求m的值；
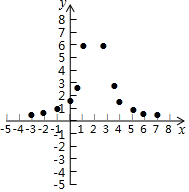
（3）如图，在平面直角坐标系xOy中，描出了以上表中各对对应值为坐标的点．根据描出的点，画出该函数的图象；
（4）结合函数的图象，写出该函数的一条性质：函数图象关于直线x=2对称．
有这样一个问题：探究函数y=$\frac{6}{（x-2）^{2}}$的图象与性质．小华根据学习函数的经验，对函数y=$\frac{6}{（x-2）^{2}}$的图象与性质进行了探究．
下面是小华的探究过程，请补充完整：
（1）函数y=$\frac{6}{（x-2）^{2}}$的自变量x的取值范围是x≠2；
（2）下表是y与x的几组对应值．
| x | … | -3 | -2 | -1 | 0 | $\frac{1}{2}$ | 1 | 3 | $\frac{7}{2}$ | 4 | 5 | 6 | 7 | … |
| y | … | $\frac{6}{25}$ | $\frac{3}{8}$ | $\frac{2}{3}$ | $\frac{3}{2}$ | $\frac{8}{3}$ | 6 | 6 | $\frac{8}{3}$ | $\frac{3}{2}$ | $\frac{2}{3}$ | $\frac{3}{8}$ | m | … |
（3）如图，在平面直角坐标系xOy中，描出了以上表中各对对应值为坐标的点．根据描出的点，画出该函数的图象；
（4）结合函数的图象，写出该函数的一条性质：函数图象关于直线x=2对称．
20．
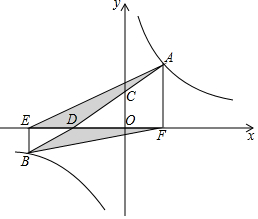如图，直线AB与双曲线y=$\frac{k}{x}$交于点A，B，与y轴交于点C，与x轴交于点D，过A，B分别作x轴的垂线AF，BE，垂足分别为点F，E，连接AE，BF，若S△ADE+S△BDF=$\frac{3}{2}$k-3，则k的值为（ ）
如图，直线AB与双曲线y=$\frac{k}{x}$交于点A，B，与y轴交于点C，与x轴交于点D，过A，B分别作x轴的垂线AF，BE，垂足分别为点F，E，连接AE，BF，若S△ADE+S△BDF=$\frac{3}{2}$k-3，则k的值为（ ）| A． | 3 | B． | 6 | C． | $\sqrt{3}-3$ | D． | 6$\sqrt{2}$ |
10．下列运算正确的是（ ）
| A． | π-3.14=0 | B． | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | C． | a3÷a=a2 | D． | a•a=2a |
17．某商店售出一件商品的利润为a元，利润率为20%，则此商品的进价为（ ）
| A． | （1+20%）a | B． | $\frac{a}{（1+20%）}$ | C． | 20%a | D． | $\frac{a}{20%}$ |
15．下列说法中错误的是（ ）
| A． | 两条对角线互相平分的四边形是平行四边形 | |
| B． | 两条对角线相等的菱形是正方形 | |
| C． | 两条对角线互相垂直的矩形是正方形 | |
| D． | 两条对角线相等的四边形是矩形 |