题目内容
1．m16可以写成（ ）| A． | m8+m8 | B． | m8•m8 | C． | m2•m8 | D． | m4•m4 |
分析 根据同底数幂相乘，底数不变指数相加对各选项分析判断即可得解．
解答 解：A、m8+m8=2m8，故本选项错误；
B、m8•m8=m8+8=m16，故本选项正确；
C、m2•m8=m2+8=m10，故本选项错误；
D、m4•m4=m4+4=m8，故本选项错误．
故选B．
点评 本题考查了同底数幂的乘法，熟记同底数幂相乘，底数不变指数相加是解题的关键．
练习册系列答案
华东师大版一课一练系列答案
相关题目
如图，△ABC和△EFD的边BC和FD在同一条直线上，顶点A，E在BF两侧，其中∠B=∠F，BD=FC．要使△ABC≌△EFD，则需要添加的一个条件时AB=EF 或∠ACB=∠EDF或AC∥DE或∠A=∠E．（只写一种即可）
5．一天时间为86400秒，用科学记数法表示这一数字是（ ）
| A． | 864×102 | B． | 86.4×103 | C． | 8.64×104 | D． | 0.864×105 |
2．下列图形中，既是轴对称图形又是中心对称图形的是（ ）
| A． |  | B． |  | C． |  | D． |  |
9．在《数据分析》章节测试中，“勇往直前”学习小组7位同学的成绩分别是92，88，95，93，96，95，94．这组数据的中位数和众数分别是（ ）
| A． | 94，94 | B． | 94，95 | C． | 93，95 | D． | 93，96 |
已知直线y=kx+b在平面直角坐标系中的位置如图所示，求该直线的函数解析式．
13．
有这样一个问题：探究函数y=$\frac{6}{（x-2）^{2}}$的图象与性质．
小华根据学习函数的经验，对函数y=$\frac{6}{（x-2）^{2}}$的图象与性质进行了探究．
下面是小华的探究过程，请补充完整：
（1）函数y=$\frac{6}{（x-2）^{2}}$的自变量x的取值范围是x≠2；
（2）下表是y与x的几组对应值．
求m的值；
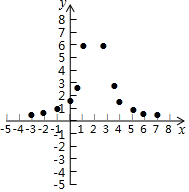
（3）如图，在平面直角坐标系xOy中，描出了以上表中各对对应值为坐标的点．根据描出的点，画出该函数的图象；
（4）结合函数的图象，写出该函数的一条性质：函数图象关于直线x=2对称．
有这样一个问题：探究函数y=$\frac{6}{（x-2）^{2}}$的图象与性质．小华根据学习函数的经验，对函数y=$\frac{6}{（x-2）^{2}}$的图象与性质进行了探究．
下面是小华的探究过程，请补充完整：
（1）函数y=$\frac{6}{（x-2）^{2}}$的自变量x的取值范围是x≠2；
（2）下表是y与x的几组对应值．
| x | … | -3 | -2 | -1 | 0 | $\frac{1}{2}$ | 1 | 3 | $\frac{7}{2}$ | 4 | 5 | 6 | 7 | … |
| y | … | $\frac{6}{25}$ | $\frac{3}{8}$ | $\frac{2}{3}$ | $\frac{3}{2}$ | $\frac{8}{3}$ | 6 | 6 | $\frac{8}{3}$ | $\frac{3}{2}$ | $\frac{2}{3}$ | $\frac{3}{8}$ | m | … |
（3）如图，在平面直角坐标系xOy中，描出了以上表中各对对应值为坐标的点．根据描出的点，画出该函数的图象；
（4）结合函数的图象，写出该函数的一条性质：函数图象关于直线x=2对称．
10．下列运算正确的是（ ）
| A． | π-3.14=0 | B． | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | C． | a3÷a=a2 | D． | a•a=2a |
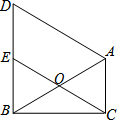如图，在△ABC中，∠ACB=90°，∠ABC=30°．O为AB的中点，连接CO并延长到E，使OE=OC．过点A作AD∥CE交BE的延长线于D．