题目内容
下列成语所描述的事件是必然发生的是（ ）
A. 水中捞月 B. 拔苗助长 C. 守株待兔 D. 瓮中捉鳖
D
【解析】试题分析：必然事件是指一定会发生的事件；不可能事件是指不可能发生的事件；随机事件是指可能发生也可能不发生的事件。根据定义，对每个选项逐一判断A选项，不可能事件 B选项，不可能事件 C选项，随机事件D选项，必然事件
（2016浙江省衢州市）已知直角坐标系内有四个点O（0，0），A（3，0），B（1，1），C（x，1），若以O，A，B，C为顶点的四边形是平行四边形，则x=____________．
4或﹣2．
【解析】试题解析：根据题意画图如下：
以O，A，B，C为顶点的四边形是平行四边形，则C（4，1）或（﹣2，1），则x=4或﹣2；故答案为：4或﹣2． 已知抛物线y＝x2－mx＋m－2.
(1)求证此抛物线与x轴有两个交点；
(2)若抛物线与x轴的一个交点为(2，0)，求m的值及抛物线与x轴另一交点坐标．
(1)证明见解析(2)抛物线与x轴另一交点坐标为(0，0)
【解析】试题分析：（1）欲证明抛物线与x轴有两个不同的交点，只要证明△＞0即可．
（2）把(2，0)代入抛物线解析式，即可得到m的值，从而得到抛物线的解析式，令y=0，解方程即可得到结论．
试题解析：【解析】
(1)∵Δ＝(－m)2－4(m－2)＝m2－4m＋8＝(m－2)2＋4＞0， ∴此抛物线与x轴有两个交点．
... 不透明的袋子中装有4个红球、3个黄球和5个蓝球，每个球除颜色不同外其它都相同，从中任意摸出一个球，则摸出__球的可能性最大．
蓝
【解析】因为袋子中有7个红球,3个黄球和5个蓝球,从中任意摸出一个球,为红球的概率是,黄球的概率是,蓝球的概率是,可见摸出蓝球的概率最大,故答案为:蓝. 下列事件为必然事件的是（ ）
A. 小王参加本次数学考试，成绩是150分
B. 某射击运动员射靶一次，正中靶心
C. 打开电视机，CCTV第一套节目正在播放新闻
D. 口袋中装有2个红球和1个白球，从中摸出2个球，其中必有红球
D
【解析】试题分析：A．小王参加本次数学考试，成绩是150分是随机事件，故A选项错误；
B．某射击运动员射靶一次，正中靶心是随机事件，故B选项错误；
C．打开电视机，中央一套节目正在播放新闻是随机事件，故C选项错误．
D．口袋中装有两个红球和一个白球，从中摸出两个球，其中必有红球是必然事件，故D选项正确；
故选D． 如图，从A地到C地，可供选择的方案是走水路、走陆路、走空中，从A地到B地有两条水路、两条陆路，从B地到C地有3条陆路可供选择，走空中，从A地不经B地直线到C地，则从A地到C地可供选择的方案有（ ）
A. 20种 B. 8种 C. 5种 D. 13种
D
【解析】此题只需分别数出A到B、B到C、A到C的条数，再进一步分析计算即可．
【解析】
观察图形，得
A到B有4条，B到C有3条，所以A到B到C有4×3=12条，A到C一条．
所以从A地到C地可供选择的方案共13条．
故选D． 如图，线段AB的长为2，C为AB上一个动点，分别以AC、BC为斜边在AB的同侧作两个等腰直角三角形△ACD和△BCE，那么DE长的最小值是______________．
4
【解析】动点问题，等腰直角三角形的性质，平角定义，勾股定理，二次函数的最值。
设AC＝x，则BC＝2－x，
∵△ACD和△BCE都是等腰直角三角形，
∴∠DCA＝45°，∠ECB＝45°，DC＝，CE＝。
∴∠DCE＝90°。
∴DE2＝DC2＋CE2＝（）2＋[]2＝x2－2x＋2＝(x－1)2＋1。
∴当x＝1时，DE2取得最小值，DE也取得最小值... 如图，△ABO中，AB⊥OB，OB=
，AB=1，把△ABO绕点O旋转150°后得到△A1B1O，则点A1的坐标为
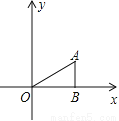
A. （﹣1，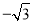 
） B. （﹣1， 
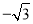）或（﹣2，0） C. （
，﹣1）或（0，﹣2） D. （
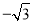，﹣1）
B
【解析】试题分析：需要分类讨论：在把△ABO绕点O顺时针旋转150°和逆时针旋转150°后得到△A1B1O时点A1的坐标，即：
∵△ABO中，AB⊥OB，OB=，AB=1，
∴tan∠AOB=，
∴∠AOB=30°．
如图1，当△ABO绕点O顺时针旋转150°后得到△A1B1O，
则∠A1OC=150°﹣∠AOB﹣∠BOC=150°﹣30°﹣90°=30°，... 如图，已知等边△AEB和等边△BDC在线段AC同侧，则下面错误的是（ ）
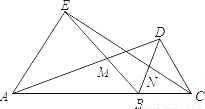
A. △ABD≌△EBC B. △NBC≌△MBD C. DM=DC D. ∠ABD=∠EBC
C
【解析】选项A，可以利用SAS验证，正确；选项B，可以利用AAS验证，正确；选项C，可证∠MBN=60°，若DM=DC=DB，则△DMB为等边三角形，即∠BDM=60°，∵∠EAB=∠DBC，∴AE∥BD．∴∠BDM=∠EAD=60°．与已知不符，错误；选项D，可由∠ABE，∠DBC同加一个∠DBE得到，正确.所以错误的是第三个,故选C.