��Ŀ����
�����¼�Ϊ��Ȼ�¼����ǣ�������
A. С���μӱ�����ѧ���ԣ��ɼ���150��
B. ij����˶�Ա���һ�Σ����а���
C. ���ӻ���CCTV��һ��Ŀ���ڲ�������
D. �ڴ���װ��2�������1������������2�������б��к���
 D
�����������������A��С���μӱ�����ѧ���ԣ��ɼ���150��������¼�����Aѡ�����
B��ij����˶�Ա���һ�Σ����а���������¼�����Bѡ�����
C�����ӻ�������һ��Ŀ���ڲ�������������¼�����Cѡ�����
D���ڴ���װ�����������һ���������������������б��к����DZ�Ȼ�¼�����Dѡ����ȷ��
��ѡD��
D
�����������������A��С���μӱ�����ѧ���ԣ��ɼ���150��������¼�����Aѡ�����
B��ij����˶�Ա���һ�Σ����а���������¼�����Bѡ�����
C�����ӻ�������һ��Ŀ���ڲ�������������¼�����Cѡ�����
D���ڴ���װ�����������һ���������������������б��к����DZ�Ȼ�¼�����Dѡ����ȷ��
��ѡD��
��ͼ���ı���ABCDΪƽ���ı��Σ���BAD�Ľ�ƽ����AE��CD�ڵ�F����BC���ӳ����ڵ�E��
��1����֤��BE=CD��
��2������BF����BF��AE����BEA=60�㣬AB=4����ƽ���ı���ABCD�������
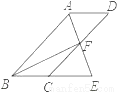
 ��1�������������2��.
�������������������1����ƽ���ı��ε����ʺͽ�ƽ������֤��BAE=��BEA�����ݵ��������ε����ʿɵ�AB=BE����2����֤��ABE�ǵȱ������Σ����ݵȱ������ε����ʿɵ�AE=AB=4��AF=EF=2���ɹ��ɶ������BF������AAS֤����ADF�ա�ECF������ADF�����=��ECF����������ƽ���ı���ABCD�����=��ABE�����=AE•BF�����ɵó������
...
��1�������������2��.
�������������������1����ƽ���ı��ε����ʺͽ�ƽ������֤��BAE=��BEA�����ݵ��������ε����ʿɵ�AB=BE����2����֤��ABE�ǵȱ������Σ����ݵȱ������ε����ʿɵ�AE=AB=4��AF=EF=2���ɹ��ɶ������BF������AAS֤����ADF�ա�ECF������ADF�����=��ECF����������ƽ���ı���ABCD�����=��ABE�����=AE•BF�����ɵó������
... ��֪���κ���y=��2x2+4x��3�����y��x���������С����ôx��ȡֵ��Χ�ǣ�������
A. x��1 B. x��0 C. x�ݩ�1 D. x�ݩ�2
 A
����������������
��y=��2x2+4x��3=��2��x��1��2��1���������߿������£��Գ���Ϊx=1���൱x��1ʱ��y��x���������С����ѡA��
A
����������������
��y=��2x2+4x��3=��2��x��1��2��1���������߿������£��Գ���Ϊx=1���൱x��1ʱ��y��x���������С����ѡA�� ���á�һ���������ܿ��ܡ����������Լ�С���������ܡ�������̫���ܡ����������ܡ������������������¼��Ŀ����ԣ�
��1����20ע��Ʊ�����صȽ�500��
��2��������20����1����ģ�19���ģ�������ȡһ��ȡ����ɫ����
��3����һö���ȵ����ӣ�6�㳯�ϣ�
��4��100����Ʒ����2����Ʒ��98����Ʒ��������ȡһ�����պ�����Ʒ��
��5���糿̫���Ӷ�������
��6��С������100m�ߣ�
 ��1�������Լ�С����2����̫���ܣ���3�����ܣ���4���ܿ��ܣ���5��һ������6��������.
������������������¼��Ŀ�������Ҫ���¼������ͣ��¼������;����˿����Լ������ԵĴ�С��
�����������1����20ע��Ʊ�����صȽ�500�����Լ�С��
��2��������20����1����ģ�19���ģ�������ȡһ��ȡ����ɫ����̫���ܣ�
��3����һö���ȵ����ӣ�6�㳯�ϣ����ܣ�
��4��100����Ʒ...
��1�������Լ�С����2����̫���ܣ���3�����ܣ���4���ܿ��ܣ���5��һ������6��������.
������������������¼��Ŀ�������Ҫ���¼������ͣ��¼������;����˿����Լ������ԵĴ�С��
�����������1����20ע��Ʊ�����صȽ�500�����Լ�С��
��2��������20����1����ģ�19���ģ�������ȡһ��ȡ����ɫ����̫���ܣ�
��3����һö���ȵ����ӣ�6�㳯�ϣ����ܣ�
��4��100����Ʒ... ��һ��3�����ѧ��50�ˣ�����������21�ˣ�Ů��29�ˣ����ڴ˰���������һ��ѧ�����ҵ������Ŀ����Ա��ҵ�Ů���Ŀ�����__�����С������
 С
��������ֻҪ�Ƚ�����������Ů�������Ķ��ټ��ɣ�
��������
������������Ů������������ҵ������Ŀ����Ա��ҵ�Ů���Ŀ�����С��
С
��������ֻҪ�Ƚ�����������Ů�������Ķ��ټ��ɣ�
��������
������������Ů������������ҵ������Ŀ����Ա��ҵ�Ů���Ŀ�����С�� ���г������������¼��DZ�Ȼ�������ǣ�������
A. ˮ������ B. �������� C. ������� D. ������
 D
�������������������Ȼ�¼���ָһ���ᷢ�����¼����������¼���ָ�����ܷ������¼�������¼���ָ���ܷ���Ҳ���ܲ��������¼������ݶ��壬��ÿ��ѡ����һ�ж�Aѡ��������¼� Bѡ��������¼� Cѡ�����¼�Dѡ���Ȼ�¼�
D
�������������������Ȼ�¼���ָһ���ᷢ�����¼����������¼���ָ�����ܷ������¼�������¼���ָ���ܷ���Ҳ���ܲ��������¼������ݶ��壬��ÿ��ѡ����һ�ж�Aѡ��������¼� Bѡ��������¼� Cѡ�����¼�Dѡ���Ȼ�¼� ������У�Ļ�У�ij��ȤС���������ͼ��ʾ��ֱ��ǽ��(�����㹻��)����28m�������Χ��һ�����λ�ABCD(���ֻΧAB��BC����)����AB��xm.
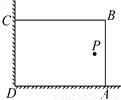
(1)���������Ϊ192m2����x��ֵ��
(2)����P����һ������ǽCD��AD�ľ���ֱ���13m��6m��Ҫ�������Χ�ڻ���(���߽磬���������Ĵ�ϸ)�������S�����ֵ��
 (1)12��16(2)��x��13ʱ��S���195
�������������������1����������ó�������=192�������ó��𰸣�
��2������P����һ������ǽCD��AD�ľ���ֱ���13m��6m�����x��ȡֵ��Χ�����ݶ��ε�������⼴��.
���������(1)(28��x)x��192�����x1��12��x2��16��
��x��ֵΪ12��16.
(2)��S��x(28��x)����x2��28x(6��x��1...
(1)12��16(2)��x��13ʱ��S���195
�������������������1����������ó�������=192�������ó��𰸣�
��2������P����һ������ǽCD��AD�ľ���ֱ���13m��6m�����x��ȡֵ��Χ�����ݶ��ε�������⼴��.
���������(1)(28��x)x��192�����x1��12��x2��16��
��x��ֵΪ12��16.
(2)��S��x(28��x)����x2��28x(6��x��1... ��ͼ,��ƽ��ֱ������ϵ��,���߶�AB�Ƶ�A����ʱ�뷽����ת90���,�õ��߶�AB',���B'������Ϊ_____.

 (4,2)
�����������������������ת���ͼ��λ�ã�����ͼ����⣮
���������AB��ת��λ����ͼ��ʾ��
B�䣨4��2����
(4,2)
�����������������������ת���ͼ��λ�ã�����ͼ����⣮
���������AB��ת��λ����ͼ��ʾ��
B�䣨4��2���� ��֪�ڡ�ABC�У�AB=AC��

��1����DΪAC���е㣬BD�������ε��ܳ���Ϊ24cm��30cm�����֣����ABC���ߵij���
��2����DΪAC��һ�㣬��˵��AC�� ��BD+DC����
��BD+DC����
 ��1�������ε����߳�Ϊ16��16��22��20��20��14����2�����ɼ�����
�������������������1��������������ۣ���AB+AD=30��BC+DC=24��AB+AD=24��BC+DC=30�����Ը��ݵ��������ε�������Ⱥ����ߵ����ʿ���ã����߳�Ϊ16��16��22��20��20��14��
��2����������������֮�ʹ��ڵ������ɵõ�AC����BD+DC��.
���������
��1����������...
��1�������ε����߳�Ϊ16��16��22��20��20��14����2�����ɼ�����
�������������������1��������������ۣ���AB+AD=30��BC+DC=24��AB+AD=24��BC+DC=30�����Ը��ݵ��������ε�������Ⱥ����ߵ����ʿ���ã����߳�Ϊ16��16��22��20��20��14��
��2����������������֮�ʹ��ڵ������ɵõ�AC����BD+DC��.
���������
��1����������... 
