��Ŀ����
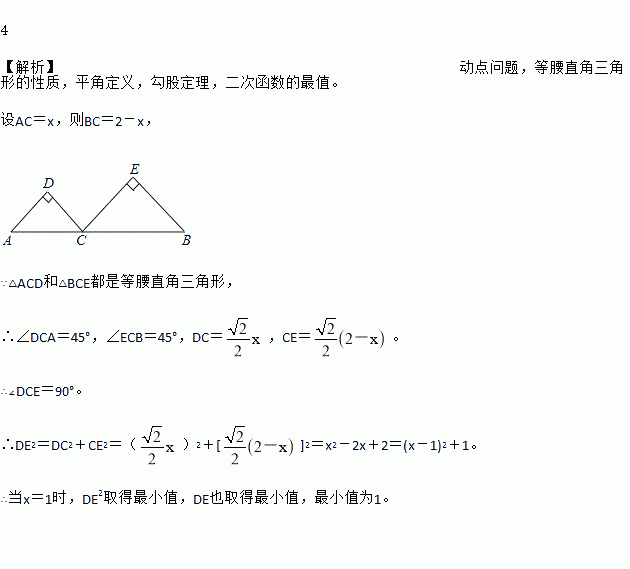
��ͼ���߶�AB�ij�Ϊ2��CΪAB��һ�����㣬�ֱ���AC��BCΪб����AB��ͬ������������ֱ�������Ρ�ACD�͡�BCE����ôDE������Сֵ��______________��

 4
���������������⣬����ֱ�������ε����ʣ�ƽ�Ƕ��壬���ɶ��������κ�������ֵ��
��AC��x����BC��2��x��
�ߡ�ACD�͡�BCE���ǵ���ֱ�������Σ�
���DCA��45�㣬��ECB��45�㣬DC����CE����
���DCE��90�㡣
��DE2��DC2��CE2������2��[]2��x2��2x��2��(x��1)2��1��
�൱x��1ʱ��DE2ȡ����Сֵ��DEҲȡ����Сֵ...
4
���������������⣬����ֱ�������ε����ʣ�ƽ�Ƕ��壬���ɶ��������κ�������ֵ��
��AC��x����BC��2��x��
�ߡ�ACD�͡�BCE���ǵ���ֱ�������Σ�
���DCA��45�㣬��ECB��45�㣬DC����CE����
���DCE��90�㡣
��DE2��DC2��CE2������2��[]2��x2��2x��2��(x��1)2��1��
�൱x��1ʱ��DE2ȡ����Сֵ��DEҲȡ����Сֵ...
��ͼ����ƽ���ı���ABCD�У���ABC��ƽ���߽�AD��E����BED=150�㣬���A�Ĵ�СΪ��������
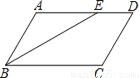
A. 150�� B. 130�� C. 120�� D. 100��
 C
��������������������ı���ABCD��ƽ���ı��Σ���AD��BC�����AEB=��CBE����BEƽ�֡�ABE�����ABE=��CBE�����AEB=��ABE����AB=AE���ߡ�BED=150�㣬���ABE=��AEB=30�㣬���A=180�㩁��ABE����AEB=120�㣮��ѡC��
C
��������������������ı���ABCD��ƽ���ı��Σ���AD��BC�����AEB=��CBE����BEƽ�֡�ABE�����ABE=��CBE�����AEB=��ABE����AB=AE���ߡ�BED=150�㣬���ABE=��AEB=30�㣬���A=180�㩁��ABE����AEB=120�㣮��ѡC�� ���á�һ���������ܿ��ܡ����������Լ�С���������ܡ�������̫���ܡ����������ܡ������������������¼��Ŀ����ԣ�
��1����20ע��Ʊ�����صȽ�500��
��2��������20����1����ģ�19���ģ�������ȡһ��ȡ����ɫ����
��3����һö���ȵ����ӣ�6�㳯�ϣ�
��4��100����Ʒ����2����Ʒ��98����Ʒ��������ȡһ�����պ�����Ʒ��
��5���糿̫���Ӷ�������
��6��С������100m�ߣ�
 ��1�������Լ�С����2����̫���ܣ���3�����ܣ���4���ܿ��ܣ���5��һ������6��������.
������������������¼��Ŀ�������Ҫ���¼������ͣ��¼������;����˿����Լ������ԵĴ�С��
�����������1����20ע��Ʊ�����صȽ�500�����Լ�С��
��2��������20����1����ģ�19���ģ�������ȡһ��ȡ����ɫ����̫���ܣ�
��3����һö���ȵ����ӣ�6�㳯�ϣ����ܣ�
��4��100����Ʒ...
��1�������Լ�С����2����̫���ܣ���3�����ܣ���4���ܿ��ܣ���5��һ������6��������.
������������������¼��Ŀ�������Ҫ���¼������ͣ��¼������;����˿����Լ������ԵĴ�С��
�����������1����20ע��Ʊ�����صȽ�500�����Լ�С��
��2��������20����1����ģ�19���ģ�������ȡһ��ȡ����ɫ����̫���ܣ�
��3����һö���ȵ����ӣ�6�㳯�ϣ����ܣ�
��4��100����Ʒ... ���г������������¼��DZ�Ȼ�������ǣ�������
A. ˮ������ B. �������� C. ������� D. ������
 D
�������������������Ȼ�¼���ָһ���ᷢ�����¼����������¼���ָ�����ܷ������¼�������¼���ָ���ܷ���Ҳ���ܲ��������¼������ݶ��壬��ÿ��ѡ����һ�ж�Aѡ��������¼� Bѡ��������¼� Cѡ�����¼�Dѡ���Ȼ�¼�
D
�������������������Ȼ�¼���ָһ���ᷢ�����¼����������¼���ָ�����ܷ������¼�������¼���ָ���ܷ���Ҳ���ܲ��������¼������ݶ��壬��ÿ��ѡ����һ�ж�Aѡ��������¼� Bѡ��������¼� Cѡ�����¼�Dѡ���Ȼ�¼� ������У�Ļ�У�ij��ȤС���������ͼ��ʾ��ֱ��ǽ��(�����㹻��)����28m�������Χ��һ�����λ�ABCD(���ֻΧAB��BC����)����AB��xm.
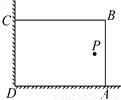
(1)���������Ϊ192m2����x��ֵ��
(2)����P����һ������ǽCD��AD�ľ���ֱ���13m��6m��Ҫ�������Χ�ڻ���(���߽磬���������Ĵ�ϸ)�������S�����ֵ��
 (1)12��16(2)��x��13ʱ��S���195
�������������������1����������ó�������=192�������ó��𰸣�
��2������P����һ������ǽCD��AD�ľ���ֱ���13m��6m�����x��ȡֵ��Χ�����ݶ��ε�������⼴��.
���������(1)(28��x)x��192�����x1��12��x2��16��
��x��ֵΪ12��16.
(2)��S��x(28��x)����x2��28x(6��x��1...
(1)12��16(2)��x��13ʱ��S���195
�������������������1����������ó�������=192�������ó��𰸣�
��2������P����һ������ǽCD��AD�ľ���ֱ���13m��6m�����x��ȡֵ��Χ�����ݶ��ε�������⼴��.
���������(1)(28��x)x��192�����x1��12��x2��16��
��x��ֵΪ12��16.
(2)��S��x(28��x)����x2��28x(6��x��1... ����ë������У�ij����ë����˶�·�߿��Կ�����������y����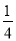 x2��bx��c��һ����(��ͼ)�����г����B�����O��ľ�����1m������ص�A��O��ľ�����4m����ô���������ߵı���ʽ��( )
x2��bx��c��һ����(��ͼ)�����г����B�����O��ľ�����1m������ص�A��O��ľ�����4m����ô���������ߵı���ʽ��( )

A. y����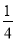 x2��
x2��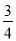 x��1 B. y����
x��1 B. y����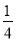 x2��
x2��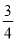 x��1 C. y����
x��1 C. y����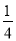 x2��
x2��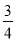 x��1 D. y����
x��1 D. y����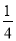 x2��
x2��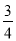 x��1
x��1
 A
��������������֪�����B�����O��ľ�����1m������ص�A��O��ľ�����4m���ó�B�������Ϊ����0��1����A������Ϊ��4��0�����������ʽy����x2��bx��c���������b=��c=1�����ɵó����������ߵĽ���ʽ�ǣ�y=-x2+x+1��
��ѡ��A��
A
��������������֪�����B�����O��ľ�����1m������ص�A��O��ľ�����4m���ó�B�������Ϊ����0��1����A������Ϊ��4��0�����������ʽy����x2��bx��c���������b=��c=1�����ɵó����������ߵĽ���ʽ�ǣ�y=-x2+x+1��
��ѡ��A�� ��ͼ,��ƽ��ֱ������ϵ��,���߶�AB�Ƶ�A����ʱ�뷽����ת90���,�õ��߶�AB',���B'������Ϊ_____.

 (4,2)
�����������������������ת���ͼ��λ�ã�����ͼ����⣮
���������AB��ת��λ����ͼ��ʾ��
B�䣨4��2����
(4,2)
�����������������������ת���ͼ��λ�ã�����ͼ����⣮
���������AB��ת��λ����ͼ��ʾ��
B�䣨4��2���� ��ͼ��һС���б��O�㴦�׳�������׳�·�߿����ö��κ���y=��x2+4x�̻���б�¿�����һ�κ���y=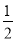 x�̻���
x�̻���
��1�������䷽������κ���ͼ�����ߵ�P�����ꣻ
��2��С��������A�����A�����ꣻ
��3�����������ߵ���ߵ�P���O��A�á�POA�����POA�������
��4����OA�Ϸ����������ϴ���һ��M��M��P���غϣ�����MOA��������ڡ�POA���������ֱ��д����M�����꣮
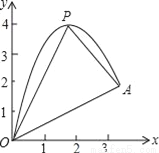
 ��1����ߵ�P������Ϊ��2��4������2����A������Ϊ���� ������3������4����M������Ϊ���� ��
�������������������1�������䷽�������ߵ�һ��ʽ��Ϊ����ʽ������������κ���ͼ�����ߵ�P�����ꣻ
��2������������ʽ�����������A�����ꣻ
��3����PQ��x���ڵ�Q��AB��x���ڵ�B������S��POA=S��POQ+S������PQBA��S��BOA��������ֵ���㼴����⣻
��4����P...
��1����ߵ�P������Ϊ��2��4������2����A������Ϊ���� ������3������4����M������Ϊ���� ��
�������������������1�������䷽�������ߵ�һ��ʽ��Ϊ����ʽ������������κ���ͼ�����ߵ�P�����ꣻ
��2������������ʽ�����������A�����ꣻ
��3����PQ��x���ڵ�Q��AB��x���ڵ�B������S��POA=S��POQ+S������PQBA��S��BOA��������ֵ���㼴����⣻
��4����P... ��֪����ͼ����ABC�У�BO��CO�ֱ��ǡ�ABC�͡�ACB��ƽ���ߣ���O���ֱ�߷ֱ�AB��AC�ڵ�D��E����DE��BC����AB=6cm��AC=8cm�����ADE���ܳ�Ϊ__��
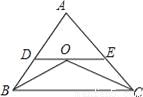

 14cm
����������ֱ��ƽ�У��ڴ�����ȣ��Լ����ݽ�ƽ�������ʣ��ɵá�OBD����EOC��Ϊ���������Σ��ɴ˰ѡ�AEF���ܳ�ת��ΪAC+AB��
��������
��DE��BC�����DOB=��OBC���֡�BO�ǡ�ABC�Ľ�ƽ���ߣ����DBO=��OBC�����DBO=��DOB����BD=OD��ͬ����OE=EC��
���ADE���ܳ�=AD+OD+OE+EC=AD+BD+AE+EC=AB+AC=14c...
14cm
����������ֱ��ƽ�У��ڴ�����ȣ��Լ����ݽ�ƽ�������ʣ��ɵá�OBD����EOC��Ϊ���������Σ��ɴ˰ѡ�AEF���ܳ�ת��ΪAC+AB��
��������
��DE��BC�����DOB=��OBC���֡�BO�ǡ�ABC�Ľ�ƽ���ߣ����DBO=��OBC�����DBO=��DOB����BD=OD��ͬ����OE=EC��
���ADE���ܳ�=AD+OD+OE+EC=AD+BD+AE+EC=AB+AC=14c...