题目内容
如图，从A地到C地，可供选择的方案是走水路、走陆路、走空中，从A地到B地有两条水路、两条陆路，从B地到C地有3条陆路可供选择，走空中，从A地不经B地直线到C地，则从A地到C地可供选择的方案有（ ）
A. 20种 B. 8种 C. 5种 D. 13种
D
【解析】此题只需分别数出A到B、B到C、A到C的条数，再进一步分析计算即可．
【解析】
观察图形，得
A到B有4条，B到C有3条，所以A到B到C有4×3=12条，A到C一条．
所以从A地到C地可供选择的方案共13条．
故选D．
如图，在△ABC中，∠ABC=90°，AB=8，BC=6．若DE是△ABC的中位线，延长DE交△ABC的外角∠ACM的平分线于点F，则线段DF的长为（ ）
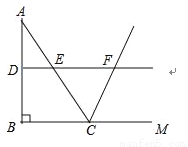
A. 7 B. 8 C. 9 D. 10
B
【解析】试题分析：在RT△ABC中，∵∠ABC=90°，AB=8，BC=6，∴AC===10，∵DE是△ABC的中位线，∴DF∥BM，DE=BC=3，∴∠EFC=∠FCM，∵∠FCE=∠FCM，∴∠EFC=∠ECF，∴EC=EF=AC=5，∴DF=DE+EF=3+5=8．故选B． 二次函数y=ax2+bx+c（a，b，c为常数，且a≠0）中的x与y的部分对应值如下表：
X | ﹣1 | 0 | 1 | 3 |
y | ﹣1 | 3 | 5 | 3 |
下列结论：
⑴ac＜0；
⑵当x＞1时，y的值随x值的增大而减小．
⑶3是方程ax2+（b﹣1）x+c=0的一个根；
⑷当﹣1＜x＜3时，ax2+（b﹣1）x+c＞0．
其中正确的个数为（ ）
A. 4个 B. 3个 C. 2个 D. 1个
B
【解析】二次函数过（-1，-1），（0,3），（1,5），
，
解得,y=-.对称轴,,
(1)正确，（2）开口向下，对称轴，x＞1时y先增大再减小,错误，（3）+2,解得， .正确，（4）+2,所以由（3）得到函数与x轴的交点，作图知，﹣1＜x＜3时,y>0正确.
所以（1）（3）（4）正确.选B. 下列事件中，是必然事件的是（ ）
A. 打开电视机，里面正在转播足球比赛 B. 小麦的亩产量一定为1000公斤
C. 在只装有5个红球的袋中摸出1球是红球 D. 在农历十五的晚上，一定能看到圆月
C
【解析】选项A，B，D选项为不确定事件，即随机事件；选项C是必然发生事件．故选C． 下列成语所描述的事件是必然发生的是（ ）
A. 水中捞月 B. 拔苗助长 C. 守株待兔 D. 瓮中捉鳖
D
【解析】试题分析：必然事件是指一定会发生的事件；不可能事件是指不可能发生的事件；随机事件是指可能发生也可能不发生的事件。根据定义，对每个选项逐一判断A选项，不可能事件 B选项，不可能事件 C选项，随机事件D选项，必然事件 如图，一座抛物线型拱桥，桥下水面宽度是4m时，拱高为2m，一艘木船宽2m.要能顺利从桥下通过，船顶点与桥拱之间的间隔应不少于0.3m，那么木船的高不得超过 ______m.
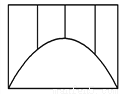
1.2
【解析】以水面所在水平线为x轴，过拱桥顶点作水平线的垂线，作为y轴，建立坐标系，设水平面与拱桥的交点为A（-2，0），B（2，0），C（0，2），利用待定系数法设函数的解析式为y=a（x+2）（x-2）代入点C坐标，求得a=-，即抛物线的解析式为y=-（x+2）（x-2），令x=1，解得y=1.5，船顶与桥拱之间的间隔应不少于0.3，则木船的最高高度为1.5-0.3=1.2米.
... 在羽毛球比赛中，某次羽毛球的运动路线可以看做是抛物线y＝－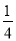
x2＋bx＋c的一部分(如图)，其中出球点B离地面O点的距离是1m，球落地点A到O点的距离是4m，那么这条抛物线的表达式是( )
A. y＝－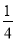
x2＋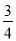
x＋1 B. y＝－
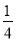x2＋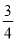
x－1 C. y＝－
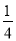x2－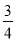
x＋1 D. y＝－
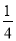x2－
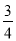x－1
A
【解析】根据已知出球点B离地面O点的距离是1m，球落地点A到O点的距离是4m，得出B点的坐标为：（0，1），A点坐标为（4，0），代入解析式y＝－x2＋bx＋c，即可求出b=，c=1，即可得出这条抛物线的解析式是：y=-x2+x+1．
故选：A． 如图，若△DEF是由△ABC经过平移后得到的，则平移的距离是（ ）
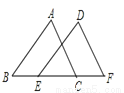
A. 线段BC的长度 B. 线段BE的长度 C. 线段EC的长度 D. 线段EF的长度
B
【解析】试题分析：对应点之间的距离就是平移的距离，根据题意可得：点B和点E对应，则线段BE的长度就是平移的距离. 已知：如图，AB＝DE，CD＝FA，∠A＝∠D，∠AFC＝∠DCF，则BC＝EF．你能说出它们相等的理由吗?
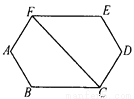
见解析
【解析】试题分析：首先连接CE、BF，然后根据条件可证明△ABF≌△DEC，再根据全等三角形的性质可得∠3=∠4，BF=EC，然后证明△BCF≌△EFC可得BC=EF．
试题解析：连接CE、BF，如图：
在△ABF和△DEC中， ，
∴△ABF≌△DEC(SAS)，
∴∠3=∠4，BF=EC，
∵∠AFC=∠DCF，
∴∠AFC?∠3=∠DCF?∠...