题目内容
已知抛物线y＝x2－mx＋m－2.
(1)求证此抛物线与x轴有两个交点；
(2)若抛物线与x轴的一个交点为(2，0)，求m的值及抛物线与x轴另一交点坐标．
(1)证明见解析(2)抛物线与x轴另一交点坐标为(0，0)
【解析】试题分析：（1）欲证明抛物线与x轴有两个不同的交点，只要证明△＞0即可．
（2）把(2，0)代入抛物线解析式，即可得到m的值，从而得到抛物线的解析式，令y=0，解方程即可得到结论．
试题解析：【解析】
(1)∵Δ＝(－m)2－4(m－2)＝m2－4m＋8＝(m－2)2＋4＞0， ∴此抛物线与x轴有两个交点．
...
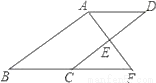
如图，E是?ABCD的边CD的中点，延长AE交BC的延长线于点F．
（1）求证：△ADE≌△FCE．
（2）若∠BAF=90°，BC=5，EF=3，求CD的长．
（1）证明过程见解析；（2）8.
【解析】试题分析：（1）由平行四边形的性质得出AD∥BC，AB∥CD，证出∠DAE=∠F，∠D=∠ECF，由AAS证明△ADE≌△FCE即可；（2）由全等三角形的性质得出AE=EF=3，由平行线的性质证出∠AED=∠BAF=90°，由勾股定理求出DE，即可得出CD的长．
试题解析：（1）∵四边形ABCD是平行四边形， ∴AD∥BC，AB∥CD，
... 如图，在平行四边形ABCD中，∠ABC的平分线交AD于E，∠BED=150°，则∠A的大小为（ ）
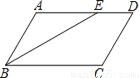
A. 150° B. 130° C. 120° D. 100°
C
【解析】试题分析：∵四边形ABCD是平行四边形，∴AD∥BC，∴∠AEB=∠CBE，∵BE平分∠ABE，∴∠ABE=∠CBE，∴∠AEB=∠ABE，∴AB=AE，∵∠BED=150°，∴∠ABE=∠AEB=30°，∴∠A=180°﹣∠ABE﹣∠AEB=120°．故选C． 抛物线y=﹣x2+bx+c上部分点的横坐标x，纵坐标y的对应值如下表所示：
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y | … | 0 | 4 | 6 | 6 | 4 | … |
从上表可知，下列说法中，错误的是（ ）
A. 抛物线与x轴的一个交点坐标为（﹣2，0） B. 抛物线与y轴的交点坐标为（0，6）
C. 抛物线的对称轴是直线x=0 D. 抛物线在对称轴左侧部分是上升的
C
【解析】【解析】
当x=﹣2时，y=0，∴抛物线过（﹣2，0），∴抛物线与x轴的一个交点坐标为（﹣2，0），故A正确；
当x=0时，y=6，∴抛物线与y轴的交点坐标为（0，6），故B正确；
当x=0和x=1时，y=6，∴对称轴为x=，故C错误；
当x＜时，y随x的增大而增大，∴抛物线在对称轴左侧部分是上升的，故D正确；
故选C． 已知二次函数y=﹣2x2+4x﹣3，如果y随x的增大而减小，那么x的取值范围是（ ）
A. x≥1 B. x≥0 C. x≥﹣1 D. x≥﹣2
A
【解析】【解析】
∵y=﹣2x2+4x﹣3=﹣2（x﹣1）2﹣1，∴抛物线开口向下，对称轴为x=1，∴当x≥1时，y随x的增大而减小．故选A． 二次函数y=ax2+bx+c（a，b，c为常数，且a≠0）中的x与y的部分对应值如下表：
X | ﹣1 | 0 | 1 | 3 |
y | ﹣1 | 3 | 5 | 3 |
下列结论：
⑴ac＜0；
⑵当x＞1时，y的值随x值的增大而减小．
⑶3是方程ax2+（b﹣1）x+c=0的一个根；
⑷当﹣1＜x＜3时，ax2+（b﹣1）x+c＞0．
其中正确的个数为（ ）
A. 4个 B. 3个 C. 2个 D. 1个
B
【解析】二次函数过（-1，-1），（0,3），（1,5），
，
解得,y=-.对称轴,,
(1)正确，（2）开口向下，对称轴，x＞1时y先增大再减小,错误，（3）+2,解得， .正确，（4）+2,所以由（3）得到函数与x轴的交点，作图知，﹣1＜x＜3时,y>0正确.
所以（1）（3）（4）正确.选B. 请用“一定”、“很可能”、“可能性极小”、“可能”、“不太可能”、“不可能”等语言来描述下列事件的可能性．
（1）买20注彩票，获特等奖500万．
（2）袋中有20个球，1个红的，19个白的，从中任取一球，取到红色的球．
（3）掷一枚均匀的骰子，6点朝上．
（4）100件产品中有2件次品，98件正品，从中任取一件，刚好是正品．
（5）早晨太阳从东方升起．
（6）小丽能跳100m高．
（1）可能性极小；（2）不太可能；（3）可能；（4）很可能；（5）一定；（6）不可能.
【解析】试题分析：事件的可能性主要看事件的类型，事件的类型决定了可能性及可能性的大小．
试题解析：（1）买20注彩票，获特等奖500万，可能性极小；
（2）袋中有20个球，1个红的，19个白的，从中任取一球，取到红色的球，不太可能；
（3）掷一枚均匀的骰子，6点朝上，可能；
（4）100件产品... 下列成语所描述的事件是必然发生的是（ ）
A. 水中捞月 B. 拔苗助长 C. 守株待兔 D. 瓮中捉鳖
D
【解析】试题分析：必然事件是指一定会发生的事件；不可能事件是指不可能发生的事件；随机事件是指可能发生也可能不发生的事件。根据定义，对每个选项逐一判断A选项，不可能事件 B选项，不可能事件 C选项，随机事件D选项，必然事件 如图，一小球从斜坡O点处抛出，球的抛出路线可以用二次函数y=﹣x2+4x刻画，斜坡可以用一次函数y=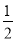
x刻画．
（1）请用配方法求二次函数图象的最高点P的坐标；
（2）小球的落点是A，求点A的坐标；
（3）连接抛物线的最高点P与点O、A得△POA，求△POA的面积；
（4）在OA上方的抛物线上存在一点M（M与P不重合），△MOA的面积等于△POA的面积．请直接写出点M的坐标．
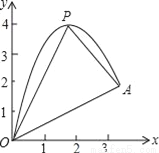
（1）最高点P的坐标为（2，4）；（2）点A的坐标为（， ）；（3）；（4）点M的坐标为（， ）
【解析】试题分析：（1）利用配方法抛物线的一般式化为顶点式，即可求出二次函数图象的最高点P的坐标；
（2）联立两解析式，可求出交点A的坐标；
（3）作PQ⊥x轴于点Q，AB⊥x轴于点B．根据S△POA=S△POQ+S△梯形PQBA﹣S△BOA，代入数值计算即可求解；
（4）过P...