题目内容
9.阅读下列材料:解答“已知x-y=2,且x>1,y<0,试确定x+y的取值范围”有如下解法:
解∵x-y=2,∴x=y+2.
又∵x>1,∴y+2>1.
∴y>-1.
又∵y<0,∴-1<y<0. …①
同理得:1<x<2. …②
由①+②得-1+1<y+x<0+2
∴x+y的取值范围是0<x+y<2
请按照上述方法,完成下列问题:
(1)已知x-y=4,且x>3,y<1,则x+y的取值范围是2<x+y<6.
(2)已知y>1,x<-1,若x-y=m成立,求x+y的取值范围(结果用含m的式子表示).
分析 (1)根据阅读材料所给的解题过程,直接套用方法与步骤解答即可;
(2)理解解题过程,按照解题思路求解.
解答 解:(1)∵x-y=4,
∴x=y+4,
又∵x>2,
∴y+3>2,
∴y>-1.
又∵y<1,
∴-1<y<1,…①
同理得:3<x<5,…②
由①+②得-1+3<y+x<1+5
∴x+y的取值范围是2<x+y<6;
(2)∵x-y=m,
∴x=y+m,
又∵x<-1,
∴y+m<-1,
∴y<-m-1,
又∵y>1,
∴1<y<-m-1,…①
同理得:m+1<x<-1,…②
由①+②得1+m+1<y+x<-m-1+(-1),
∴x+y的取值范围是m+2<x+y<-m-2.
点评 本题考查了一元一次不等式组的应用,解答本题的关键是仔细阅读材料,理解解题过程,难度一般.

练习册系列答案
 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
 小明在玩一种叫“掷飞镖”的游戏,如果小明将镖随意投中如图所示的正方形木板,那么镖落在阴影部分的概率是$\frac{1}{9}$.
小明在玩一种叫“掷飞镖”的游戏,如果小明将镖随意投中如图所示的正方形木板,那么镖落在阴影部分的概率是$\frac{1}{9}$.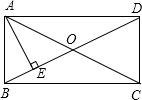 如图,在矩形ABCD中,对角线AC,BD交于点O,AE⊥BD于点E,∠AOB=50°,则∠BAE的度数是25°.
如图,在矩形ABCD中,对角线AC,BD交于点O,AE⊥BD于点E,∠AOB=50°,则∠BAE的度数是25°.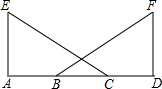 如图,已知点A,B,C,D在同一条直线上,EA⊥AB,FD⊥AD,AB=CD,若用“HL”证明Rt△AEC≌△Rt△DFB,需添加什么条件?并写出你的证明过程.
如图,已知点A,B,C,D在同一条直线上,EA⊥AB,FD⊥AD,AB=CD,若用“HL”证明Rt△AEC≌△Rt△DFB,需添加什么条件?并写出你的证明过程.