题目内容
1.已知:正方形ABCD,AB=$\sqrt{2}$,点P满足PD=1,且∠BPD=90°,过点A作AM⊥BP,垂足为点M,则AM的长为$\frac{\sqrt{3}-1}{2}$或$\frac{\sqrt{3}+1}{2}$.分析 分类讨论:当BP和BA在BD同旁,如图1,BP交AD于E,先证明Rt△ABE∽Rt△PDE,利用相似比得到BE=$\sqrt{2}$DE,设DE=x,则BE=$\sqrt{2}$x,AE=$\sqrt{2}$-x,再在Rt△ABE中利用勾股定理得到($\sqrt{2}$)2+($\sqrt{2}$-x)2=($\sqrt{2}$x)2,解得x=$\sqrt{6}$-$\sqrt{2}$,则AE=2$\sqrt{2}$-$\sqrt{6}$,BE=2$\sqrt{3}$-2,然后利用面积法求AM;当BP和BA在BD两旁,如图2,BP交CD于E,同样可证Rt△BCE∽Rt△DPE得到BE=$\sqrt{2}$DE,设DE=x,则BE=$\sqrt{2}$x,CE=$\sqrt{2}$-x,在Rt△BCE中,利用勾股定理得到($\sqrt{2}$)2+($\sqrt{2}$-x)2=($\sqrt{2}$x)2,解得x=$\sqrt{6}$-$\sqrt{2}$,则BE=2$\sqrt{3}$-2,再证明Rt△ABM∽Rt△BEC,然后利用相似比可计算出AM.
解答 解:当BP和BA在BD同旁,如图1,BP交AD于E,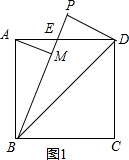 ∵∠AEB=∠PED,
∵∠AEB=∠PED,
∴Rt△ABE∽Rt△PDE,
∴$\frac{BE}{DE}$=$\frac{AB}{PD}$=$\frac{\sqrt{2}}{1}$,
∴BE=$\sqrt{2}$DE,
设DE=x,则BE=$\sqrt{2}$x,AE=$\sqrt{2}$-x,
在Rt△ABE中,($\sqrt{2}$)2+($\sqrt{2}$-x)2=($\sqrt{2}$x)2,解得x=$\sqrt{6}$-$\sqrt{2}$,
∴AE=2$\sqrt{2}$-$\sqrt{6}$,BE=2$\sqrt{3}$-2,
∵$\frac{1}{2}$AM•BE=$\frac{1}{2}$AB•AE,
∴AM=$\frac{\sqrt{2}(2\sqrt{2}-\sqrt{6})}{2\sqrt{3}-2}$=$\frac{\sqrt{3}-1}{2}$;
当BP和BA在BD两旁,如图2,BP交CD于E,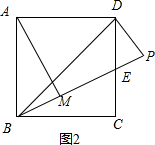 同样可证Rt△BCE∽Rt△DPE得到BE=$\sqrt{2}$DE,
同样可证Rt△BCE∽Rt△DPE得到BE=$\sqrt{2}$DE,
设DE=x,则BE=$\sqrt{2}$x,CE=$\sqrt{2}$-x,
在Rt△BCE中,($\sqrt{2}$)2+($\sqrt{2}$-x)2=($\sqrt{2}$x)2,解得x=$\sqrt{6}$-$\sqrt{2}$,
∴BE=2$\sqrt{3}$-2,
∵∠CBE=∠BAM,
∴Rt△ABM∽Rt△BEC,
∴$\frac{AM}{BC}$=$\frac{AB}{BE}$,即$\frac{AM}{\sqrt{2}}$=$\frac{\sqrt{2}}{2\sqrt{3}-2}$,
∴AM=$\frac{\sqrt{3}+1}{2}$,
综上所述,AM的长为$\frac{\sqrt{3}-1}{2}$或$\frac{\sqrt{3}+1}{2}$.
故答案为$\frac{\sqrt{3}-1}{2}$或$\frac{\sqrt{3}+1}{2}$.
点评 本题考查了正方形的性质:正方形的四条边都相等,四个角都是直角;正方形的两条对角线相等,互相垂直平分,并且每条对角线平分一组对角;正方形具有四边形、平行四边形、矩形、菱形的一切性质.也考查了相似三角形的判定与性质.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 4 | B. | 6 | C. | 9 | D. | $\frac{2}{3}$ |
 没有量角器,利用刻度尺或三角板也能画出一个角的平分线吗?下面是小彬的做法,他的画法正确吗?请说明理由.
没有量角器,利用刻度尺或三角板也能画出一个角的平分线吗?下面是小彬的做法,他的画法正确吗?请说明理由.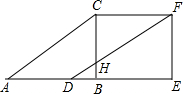 将Rt△ABC沿直角边AB向右平移2个单位得到Rt△DEF,如图,若AB=4,∠ABC=90°,且△ABC的面积为6个平方单位,求:
将Rt△ABC沿直角边AB向右平移2个单位得到Rt△DEF,如图,若AB=4,∠ABC=90°,且△ABC的面积为6个平方单位,求: