题目内容
18.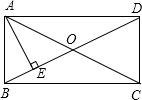 如图,在矩形ABCD中,对角线AC,BD交于点O,AE⊥BD于点E,∠AOB=50°,则∠BAE的度数是25°.
如图,在矩形ABCD中,对角线AC,BD交于点O,AE⊥BD于点E,∠AOB=50°,则∠BAE的度数是25°.
分析 易证∠BAE=∠ADE,根据矩形对角线相等且互相平分的性质,可得∠OAB=∠OBA,在Rt△ABD中,已知∠OBA即可求得∠BAE的大小.
解答 解:∵四边形ABCD是矩形,AE⊥BD,
∴∠BAE+∠ABD=90°,∠ADE+∠ABD=90°,
∴∠BAE=∠ADE,
∵矩形对角线相等且互相平分,
∴OA=OD,
∴∠OAB=∠OBA=$\frac{180°-50°}{2}$=65°,
∴∠BAE=∠ADE=90°-65°=25°,
故答案为:25°.
点评 本题考查了矩形对角线相等且互相平分的性质,考查了等腰三角形底角相等的性质,本题中计算∠OAB的值是解题的关键.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
8.妈妈开了一家服装店,读七年级的小惠想用所学(数据的分析)的知识帮妈妈分析怎样进货,在进行市场占有率的调查时,她最应该关心的是( )
| A. | 服装型号的平均数 | B. | 服装型号的众数 | ||
| C. | 服装型号的中位数 | D. | 最小的服装型号 |
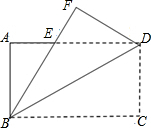 如图所示,把矩形ABCD沿对角线BD折叠,点C落在点F处,若AB=12cm,BC=16cm.
如图所示,把矩形ABCD沿对角线BD折叠,点C落在点F处,若AB=12cm,BC=16cm.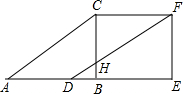 将Rt△ABC沿直角边AB向右平移2个单位得到Rt△DEF,如图,若AB=4,∠ABC=90°,且△ABC的面积为6个平方单位,求:
将Rt△ABC沿直角边AB向右平移2个单位得到Rt△DEF,如图,若AB=4,∠ABC=90°,且△ABC的面积为6个平方单位,求: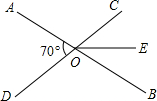 如图,直线AB、CD相交于点O,∠AOD=70°,OE平分∠BOC,求∠DOE的度数.
如图,直线AB、CD相交于点O,∠AOD=70°,OE平分∠BOC,求∠DOE的度数.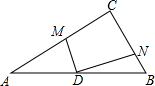 在△ABC中,∠C=90°,D为AB的中点,过点D作DM⊥DN,使DM交AC于M,DN交BC于N,求证:MN2=BN2+AM2.
在△ABC中,∠C=90°,D为AB的中点,过点D作DM⊥DN,使DM交AC于M,DN交BC于N,求证:MN2=BN2+AM2.