Question

14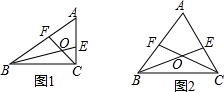．△ABC中，∠A=60°，BE，CF分别是∠ABC和∠ACB的平分线，CF与BE相交于点O．
（1）如图1，若∠ACB=90°，求证：BF+CE=BC；
（2）如图2，若∠ABC与∠ACB是任意角度，（1）中的结论是否仍成立？请说明你的理由．

Answer 1

分析 （1）在BC上找到D，使得BF=BD，根据SAS易证△BOF≌△BOD，可得∠BOF=∠BOD=60°，进而得出∠COE=∠COD=60°，即可证明△OCE≌△OCD，可得CF=CD，根据BC=BD+CD即可得出结论；
（2）在BC上找到D，使得BF=BD，易证△BOF≌△BOD，可得∠BOF=∠BOD=60°，进而得出∠COE=∠COD=60°，即可证明△OCE≌△OCD，可得CF=CD，根据BC=BD+CD即可得出结论．

解答 解：（1）在BC上找到D，使得BF=BD，
∵∠A=60°，∠ACB=90°，
∴∠ABC=30°，
∵BE，CF分别是∠ABC和∠ACB的平分线，
∴∠FBO=∠CBO=15°，∠ECO=∠BCO=45°，
∴△BOC中，∠BOC=120°，
∴∠BOF=∠COE=60°，
由BF=BD，∠FBO=∠CBO，BO=BO可得
△BOD≌△BOF（SAS），
∴∠BOD=∠BOF=60°，
∴∠COD=180°-60°-60°=60°，
∴∠COD=∠COE，
由∠COD=∠COE，CO=CO，∠ECO=∠BCO可得
∴△OCE≌△OCD（ASA），
∴CE=CD，
∵BC=BD+CD，
∴BC=BF+CE．

（2）结论BC=BF+CE仍成立．
在BC上找到D，使得BF=BD，
∵∠A=60°，BD、CE是△ABC的角平分线，
∴∠BOC=180°-$\frac{1}{2}$（∠ABC+∠ACB）=180°-$\frac{1}{2}$（180°-∠A）=120°，∠ECO=∠BCO，
∴∠BOF=∠COE=60°，
由BF=BD，∠FBO=∠CBO，BO=BO可得
△BOD≌△BOF（SAS），
∴∠BOD=∠BOF=60°，
∴∠COD=180°-60°-60°=60°，
∴∠COD=∠COE，
由∠COD=∠COE，CO=CO，∠ECO=∠BCO可得
∴△OCE≌△OCD（ASA），
∴CE=CD，
∵BC=BD+CD，
∴BC=BF+CE．

点评 本题主要考查了全等三角形的判定与性质，本题中两次判定三角形全等是解题的关键．解题时注意：两边及其夹角分别对应相等的两个三角形全等；两角及其夹边分别对应相等的两个三角形全等．