题目内容
2.已知,如图,AB∥CD,分别探讨下面四个图形中∠APC与∠PAB,∠PCD之间的关系,请你从所得到的关系中任选一个加以证明(温馨提示:添加适当辅助线)
(1)在图1中,∠APC与∠PAB,∠PCD之间的关系是:∠APC+∠PAB+∠PCD=360°.
(2)在图2中,∠APC与∠PAB,∠PCD之间的关系是:∠APC=∠PAB+∠PCD.
(3)在图3中,∠APC与∠PAB,∠PCD之间的关系是:∠PAB=∠APC+∠PCD.
(4)在图4中,∠APC与∠PAB,∠PCD之间的关系是:∠PCD=∠APC+∠PAB.
(5)在图2中,求证:∠APC=∠PAB+∠PCD.
分析 (1)首先过点P作PE∥AB,由AB∥CD,即可得AB∥PE∥CD,然后根据两直线平行,同旁内角互补,即可求得答案;
(2)首先过点P作PE∥AB,由AB∥CD,即可得AB∥PE∥CD,然后根据两直线平行,内错角相等,即可求得答案;
(3)由AB∥CD,根据两直线平行,同位角线相等,以及三角形外角的性质,即可求得答案;
(4)由AB∥CD,根据两直线平行,同位角线相等,以及三角形外角的性质,即可求得答案.
解答  解:(1)∠APC+∠PAB+∠PCD=360°;
解:(1)∠APC+∠PAB+∠PCD=360°;
(2)∠APC=∠PAB+∠PCD;
(3)∠PAB=∠APC+∠PCD;
(4)∠PCD=∠APC+∠PAB.
(5)在图2中,求证:∠APC=∠PAB+∠PCD.
证明:过P点作PE∥AB,
∴∠1=∠PAB.
又∵AB∥CD,
PE∥CD,
∴∠2=∠PCD,
∴∠1+∠2=∠PAB+∠PCD,
而∠APC=∠1+∠2,
∴∠APC=∠PAB+∠PCD.
故答案为:(1)∠APC+∠PAB+∠PCD=360°;
(2)∠APC=∠PAB+∠PCD;
(3)∠PAB=∠APC+∠PCD;
(4)∠PCD=∠APC+∠PAB.
(5)在图2中,求证:∠APC=∠PAB+∠PCD.
点评 此题考查了平行线的性质与三角形外角的性质.解题的关键是掌握两直线平行,同旁内角互补,两直线平行,内错角相等以及两直线平行,同位角相等定理的应用与辅助线的作法.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
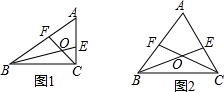 △ABC中,∠A=60°,BE,CF分别是∠ABC和∠ACB的平分线,CF与BE相交于点O.
△ABC中,∠A=60°,BE,CF分别是∠ABC和∠ACB的平分线,CF与BE相交于点O.