题目内容
9.已知二次函数y=$\frac{1}{2}$x2-(m-2)x+$\frac{m}{2}$的图象经过(-1,6),(1)求m的值并在平面直角坐标系中画出该二次函数的图象;
(2)设此二次函数的图象与x 轴的交点为A、B(A在B右边),与y轴交于点C,P在抛物线的对称轴上,当∠APC=90°时,求P点的坐标.
分析 (1)将点(-1,6)代入抛物线中即可求出m的值,也就得出了抛物线的解析式.
(2)根据解析式求得A、C的坐标以及对称轴,然后设P(3,n),根据题意得出$\frac{5-3}{\frac{5}{2}-n}$=$\frac{-n}{3}$,即可求得P的坐标.
解答 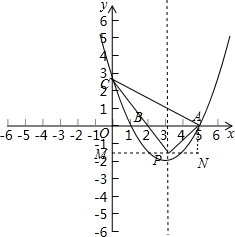 解:(1)∵二次函数y=$\frac{1}{2}$x2-(m-2)x+$\frac{m}{2}$的图象经过(-1,6),
解:(1)∵二次函数y=$\frac{1}{2}$x2-(m-2)x+$\frac{m}{2}$的图象经过(-1,6),
∴6=$\frac{1}{2}$+(m-2)+$\frac{m}{2}$,
∴m=5,
∴y=$\frac{1}{2}$x2-3x+$\frac{5}{2}$,
(2)令y=0,则$\frac{1}{2}$x2-3x+$\frac{5}{2}$=0,
解得x1=1,x2=5,
∴A(5,0),B(1,0),
令x=0,则y=$\frac{5}{2}$,
∴C(0,$\frac{5}{2}$),
∵y=$\frac{1}{2}$x2-3x+$\frac{5}{2}$,
∴对称轴x=3,
∵P在抛物线的对称轴上,
设P(3,n),
当∠APC=90°时,
∴$\frac{5-3}{\frac{5}{2}-n}$=$\frac{-n}{3}$
解得n=-$\frac{3}{2}$或n=4,
∴P(3,-$\frac{3}{2}$)或(3,4).
点评 本题考查了二次函数的性质、三角形相似的判定和性质.利用已知进行分类讨论得出符合要求点的坐标是解题关键.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
20.将一元二次方程x2-6x=2化成(x+h)2=k的形式,则k等于( )
| A. | -7 | B. | 9 | C. | 11 | D. | 5 |
4.下列调查中,适宜采用全面调查的是( )
| A. | 了解一批炮弹的杀伤半径 | |
| B. | 了解一批灯泡的使用寿命 | |
| C. | 了解全国人民对政府惩治腐败的满意程度 | |
| D. | 了解本班同学对星期天外出旅游的态度 |
 如图所示,OE平分∠AOB,OD平分∠BOC,∠AOB=90°,∠EOD=80°,则∠BOC的度数为70°.
如图所示,OE平分∠AOB,OD平分∠BOC,∠AOB=90°,∠EOD=80°,则∠BOC的度数为70°.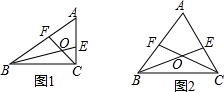 △ABC中,∠A=60°,BE,CF分别是∠ABC和∠ACB的平分线,CF与BE相交于点O.
△ABC中,∠A=60°,BE,CF分别是∠ABC和∠ACB的平分线,CF与BE相交于点O.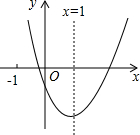 二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为x=1,给出下列结论:①abc>0;②b2=4ac;③4a+2b+c>0;④3a+c>0,其中正确的结论是①④.(写出正确命题的序号)
二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为x=1,给出下列结论:①abc>0;②b2=4ac;③4a+2b+c>0;④3a+c>0,其中正确的结论是①④.(写出正确命题的序号)