题目内容
4.若m是方程x2+x-1=0的一个根,试求代数式m3+2m2+2015的值.分析 根据一元二次方程的解的定义,将x=m代入已知方程求得m(m+1)=1;然后将所求的代数式转化为含有m(m+1)的代数式,并代入求值即可.
解答 解:根据题意,得
m2+m-1=0,
∴m2+m=1,或m(m+1)=1,
∴m3+2m2+2015=m(m2+m+m)+2015=m(m+1)+2015=1+2015=2016.即m3+2m2+2015=2016.
点评 本题主要考查了方程的解的定义.此类题型的特点是:利用方程解的定义找到相等关系,再把所求的代数式化简后整理出所找到的相等关系的形式,再把此相等关系整体代入所求代数式,即可求出代数式的值.

练习册系列答案
相关题目
13.一个六边形共有n条对角线,则n的值为( )
| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
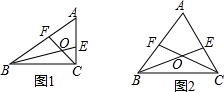 △ABC中,∠A=60°,BE,CF分别是∠ABC和∠ACB的平分线,CF与BE相交于点O.
△ABC中,∠A=60°,BE,CF分别是∠ABC和∠ACB的平分线,CF与BE相交于点O.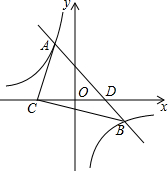 如图,一次函数y=ax+b的图象与反比例函数y=-$\frac{3}{x}$的图象交于A(-1,m)、B(3,n)两点,与x轴交于D点,且C、D两点关于y轴对称.
如图,一次函数y=ax+b的图象与反比例函数y=-$\frac{3}{x}$的图象交于A(-1,m)、B(3,n)两点,与x轴交于D点,且C、D两点关于y轴对称. 如图,抛物线y=mx2-4m(m>0)与x轴交于A、B两点,与y轴交于C点,OC=2OA.
如图,抛物线y=mx2-4m(m>0)与x轴交于A、B两点,与y轴交于C点,OC=2OA. 如图,六边形ABCDEF中,AF∥CD,AB∥DE,∠A=140°,∠B=100°,∠E=90°,求:∠C、∠D、∠F的度数.
如图,六边形ABCDEF中,AF∥CD,AB∥DE,∠A=140°,∠B=100°,∠E=90°,求:∠C、∠D、∠F的度数.