题目内容
 已知:△DBC和等边△ABC都内接于⊙O,BC=a,∠BCD=75°.(如图),求BD的长.
已知:△DBC和等边△ABC都内接于⊙O,BC=a,∠BCD=75°.(如图),求BD的长.考点:圆周角定理,等边三角形的性质,解直角三角形
专题:
分析:首先求出∠D=60°,然后运用正弦定理列出比例式
=
,即可解决问题.
| BD |
| sin∠BCD |
| BC |
| sin∠D |
解答: 解:∵△ABC是等边三角形,
解:∵△ABC是等边三角形,
∴∠A=60°;
由圆周角定理的推论知:
∠D=∠A=60°;
由正弦定理得:
=
,
∴BD=
×a
=
×a
=
a.
 解:∵△ABC是等边三角形,
解:∵△ABC是等边三角形,∴∠A=60°;
由圆周角定理的推论知:
∠D=∠A=60°;
由正弦定理得:
| BD |
| sin∠BCD |
| BC |
| sin∠D |
∴BD=
| sin75° |
| sin60° |
=
| ||||
2
|
=
| ||||
| 6 |
点评:该命题以圆为载体,以考查圆周角定理及其推论、正弦定理等几何知识点为核心构造而成;解题的关键是灵活运用有关定理来分析、判断、推理或解答.

练习册系列答案
相关题目
 如图,圆内接△ABC的外角∠MAB的平分线交圆于E,EC=8cm.求BE的长.
如图,圆内接△ABC的外角∠MAB的平分线交圆于E,EC=8cm.求BE的长.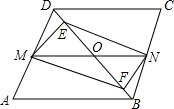 如图,在?ABCD中,点E、F在对角线BD上,DE=BF.
如图,在?ABCD中,点E、F在对角线BD上,DE=BF. △ABC中,AB=AC,AD∥BC,E在AB上,若DE=DC,求证:∠AED=∠BCE.
△ABC中,AB=AC,AD∥BC,E在AB上,若DE=DC,求证:∠AED=∠BCE.