题目内容
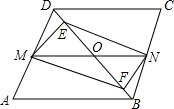 如图,在?ABCD中,点E、F在对角线BD上,DE=BF.
如图,在?ABCD中,点E、F在对角线BD上,DE=BF.(1)点O是BD的中点,直线MN过点O与AD相交于点M,与BC相交于点N,连接MF、FN、NE、ME.求证:四边形MFNE是平行四边形;
(2)M、N分别是AD、BC上的点,AM=CN,连接MF、FN、NE、ME.求证:四边形MFNE是平行四边形.
考点:平行四边形的判定与性质
专题:证明题
分析:(1)根据“对角线互相平分的四边形为平行四边形”证得结论;
(2)通过△DOM≌△BON得到OD=OB,则点O是BD的中点,结合(1)的结论,证得四边形MFNE是平行四边形.
(2)通过△DOM≌△BON得到OD=OB,则点O是BD的中点,结合(1)的结论,证得四边形MFNE是平行四边形.
解答:证明:(1) ∵四边形ABCD是平行四边形,点O是对角线BD的中点,MN过点OP,
∵四边形ABCD是平行四边形,点O是对角线BD的中点,MN过点OP,
∴OD=OB,OM=ON.
又∵DE=BF,
∴OD-DE=OB-BF,即OE=OF,
∴四边形MFNE是平行四边形;
(2)∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∵AM=CN,∠MDO=∠NBO.
∴DM=BN.
在△DOM与△BON中,
,
∴△DOM≌△BON(AAS),
∴OD=OB,
∴点O是对角线BD的中点,
∴由(1)知,四边形MFNE是平行四边形.
 ∵四边形ABCD是平行四边形,点O是对角线BD的中点,MN过点OP,
∵四边形ABCD是平行四边形,点O是对角线BD的中点,MN过点OP,∴OD=OB,OM=ON.
又∵DE=BF,
∴OD-DE=OB-BF,即OE=OF,
∴四边形MFNE是平行四边形;
(2)∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∵AM=CN,∠MDO=∠NBO.
∴DM=BN.
在△DOM与△BON中,
|
∴△DOM≌△BON(AAS),
∴OD=OB,
∴点O是对角线BD的中点,
∴由(1)知,四边形MFNE是平行四边形.
点评:本题考查了平行四边形的判定与性质.若要证明两直线平行和两线段相等、两角相等,可考虑将要证的直线、线段、角、分别置于一个四边形的对边或对角的位置上,通过证明四边形是平行四边形达到上述目的.

练习册系列答案
相关题目
正六边形的边长为
,则它的半径是( )
| 3 |
A、
| ||
| B、2 | ||
| C、3 | ||
D、2
|
下列说法正确的是( )
| A、到线段两个端点距离相等的点叫做线段的中点 |
| B、线段的中点可以有两个 |
| C、线段的中点到线段两个端点的距离相等 |
| D、线段的中点不一定是线段中的一点 |
 已知:△DBC和等边△ABC都内接于⊙O,BC=a,∠BCD=75°.(如图),求BD的长.
已知:△DBC和等边△ABC都内接于⊙O,BC=a,∠BCD=75°.(如图),求BD的长.