题目内容
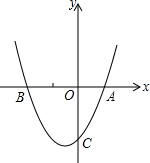 已知二次函数y=ax2+bx+c(a>0)的图象与x轴的一个交点为A(1,0),
已知二次函数y=ax2+bx+c(a>0)的图象与x轴的一个交点为A(1,0),另一个交点为B,与y轴的交点为C(0,-2).
(1)b=
(2)若a<2,试证明二次函数图象的顶点一定在第三象限;
(3)若a=1,点P是抛物线在x轴下方的一个动点(不与C重合),连结PB,PC,设所得△PBC的面积为S,试求S的取值范围.
考点:二次函数综合题,不等式的性质
专题:作图题,证明题
分析:(1)将已知点C,A代入抛物线解析式进而求出B点坐标以及b的值;
(2)根据题意证明顶点的横纵坐标均为负数,即可证明顶点一定在第三象限;
(3)首先分割四边形为S=S△POB+S△POC-S△BOC,根据三角形面积计算公式即可得出.
(2)根据题意证明顶点的横纵坐标均为负数,即可证明顶点一定在第三象限;
(3)首先分割四边形为S=S△POB+S△POC-S△BOC,根据三角形面积计算公式即可得出.
解答: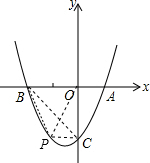 (1)解:∵二次函数y=ax2+bx+c(a>0)的图象与x轴的一个交点为A(1,0),
(1)解:∵二次函数y=ax2+bx+c(a>0)的图象与x轴的一个交点为A(1,0),
∴a+b+c=0,
∵图象与y轴的交点为:C(0,-2),
∴c=-2,
∴b=2-a,
则抛物线解析式为:y=ax2+(2-a)x-2,
y=0时,0=ax2+(2-a)x-2,
解得:x1=1,x2=-
,
∴B点坐标为:(-
,0),
故答案为:2-a,(-
,0);
(2)证明:∵二次函数图象过(1,0)点,且与y轴的交点坐标是(0,-2),
∴可(1)得:c=-2,b=2-a,
∴y=ax2+(2-a)x-2=a(x+
)2-
,
∴抛物线顶点坐标为:(-
,-
)
∵0<a<2,
∴2a>0,4a>0,2-a>0,(a+2)2>0,
∴-
<0,-
<0.
∴该二次函数图象的顶点一定在第三象限.
(3)解:当a=1时,y=x2+x-2,此时点B的坐标为(-2,0).
当0<x<1时,0<S<S△ABC,
∵S△ABC=
×AB×OC=
×3×2=3,
∴此时,0<S<3.
当-2<x<0时,可设点P的坐标为:(x,x2+x-2)
连结PO,则S=S△POB+S△POC-S△BOC
∴S=
×2×(-x2-x+2)+
×2×(-x)-
×2×2
=-x2-2x
=-(x+1)2+1,
∵当x=-1时,S取最大值1,且满足-2<-1<0,
∴此时,0<S≤1.
综上所述,S的取值范围为0<S<3.
 (1)解:∵二次函数y=ax2+bx+c(a>0)的图象与x轴的一个交点为A(1,0),
(1)解:∵二次函数y=ax2+bx+c(a>0)的图象与x轴的一个交点为A(1,0),∴a+b+c=0,
∵图象与y轴的交点为:C(0,-2),
∴c=-2,
∴b=2-a,
则抛物线解析式为:y=ax2+(2-a)x-2,
y=0时,0=ax2+(2-a)x-2,
解得:x1=1,x2=-
| 2 |
| a |
∴B点坐标为:(-
| 2 |
| a |
故答案为:2-a,(-
| 2 |
| a |
(2)证明:∵二次函数图象过(1,0)点,且与y轴的交点坐标是(0,-2),
∴可(1)得:c=-2,b=2-a,
∴y=ax2+(2-a)x-2=a(x+
| 2-a |
| 2a |
| (a+2)2 |
| 4a |
∴抛物线顶点坐标为:(-
| 2-a |
| 2a |
| (a+2)2 |
| 4a |
∵0<a<2,
∴2a>0,4a>0,2-a>0,(a+2)2>0,
∴-
| 2-a |
| 2a |
| (a+2)2 |
| 4a |
∴该二次函数图象的顶点一定在第三象限.
(3)解:当a=1时,y=x2+x-2,此时点B的坐标为(-2,0).
当0<x<1时,0<S<S△ABC,
∵S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
∴此时,0<S<3.
当-2<x<0时,可设点P的坐标为:(x,x2+x-2)
连结PO,则S=S△POB+S△POC-S△BOC
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=-x2-2x
=-(x+1)2+1,
∵当x=-1时,S取最大值1,且满足-2<-1<0,
∴此时,0<S≤1.
综上所述,S的取值范围为0<S<3.
点评:此题主要考查了二次函数综合应用以及一元二次方程解法和三角形面积求法等知识,正确分割四边形以及利用配方法求出二次函数顶点坐标是解题关键.

练习册系列答案
相关题目
某数学活动小组的20位同学站成一列报数游戏,规则是:从前面第一位同学开始,每位同学依次报自己顺序数的倒数加1,第1位同学报(
+1),第2位同学报(
+1),第3位同学报(
+1)…这样得到的20个数的积为( )
| 1 |
| 1 |
| 1 |
| 2 |
| 1 |
| 3 |
| A、19 | B、20 | C、21 | D、22 |
某市区一周的一氧化碳污染指数的数据为14,36,39,23,14,32,24,则这组数据的众数、中位数、平均数依次为( )
| A、14,24,26 |
| B、39,26,24 |
| C、14,24,24 |
| D、39,24,36 |
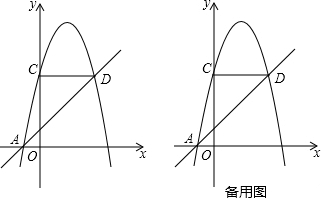
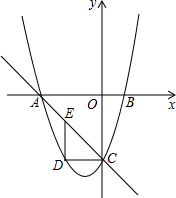 已知抛物线与x轴交于A(-3,0)、B(1,0)两点,交y轴于点C(0,-3),点E为直线AC上的一动点,DE∥y轴交抛物线于点D.
已知抛物线与x轴交于A(-3,0)、B(1,0)两点,交y轴于点C(0,-3),点E为直线AC上的一动点,DE∥y轴交抛物线于点D.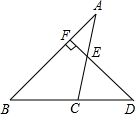 如图,已知D为△ABC边BC延长线上一点,DF⊥AB于F交AC于E,∠A=30°,∠D=55°,求∠ACD的度数.
如图,已知D为△ABC边BC延长线上一点,DF⊥AB于F交AC于E,∠A=30°,∠D=55°,求∠ACD的度数.