题目内容
阅读理解:
方程ax2+bx+c=0(a≠0)的根是x=
.方程y2+by+ac=0的根是x=
.
因此,要求ax2+bx+c=0(a≠0)的根,只要求出方程y2+by+ac=0的根,再除以a就可以了.
举例:解方程72x2+8x+
=0.
解:先解方程y2+8y+72×
=0,得y1=-2,y2=-6.
∴方程72x2+8x+
=0的两根是x1=
,x2=
.
即x1=-
,x2=-
.
请按上述阅读理解中所提供的方法解方程49x2+6x-
=0.
方程ax2+bx+c=0(a≠0)的根是x=
-b±
| ||
| 2a |
-b±
| ||
| 2 |
因此,要求ax2+bx+c=0(a≠0)的根,只要求出方程y2+by+ac=0的根,再除以a就可以了.
举例:解方程72x2+8x+
| 1 |
| 6 |
解:先解方程y2+8y+72×
| 1 |
| 6 |
∴方程72x2+8x+
| 1 |
| 6 |
| -2 |
| 72 |
| -6 |
| 72 |
即x1=-
| 1 |
| 36 |
| 1 |
| 12 |
请按上述阅读理解中所提供的方法解方程49x2+6x-
| 1 |
| 7 |
考点:解一元二次方程-公式法
专题:阅读型
分析:根据阅读材料中的方法计算即可求出解.
解答:解:先解方程y2+6y-49×
=0,即y2+6y-7=0,
分解因式得:(y-1)(y+7)=0,
解得:y1=1,y2=-7,
∴方程49x2+6x-
=0
解为:x1=
,x2=-
.
| 1 |
| 7 |
分解因式得:(y-1)(y+7)=0,
解得:y1=1,y2=-7,
∴方程49x2+6x-
| 1 |
| 7 |
解为:x1=
| 1 |
| 49 |
| 1 |
| 7 |
点评:此题考查了解一元二次方程-公式法,弄清题中的方法是解本题的关键.

练习册系列答案
 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
若一元二次方程式4x2+12x-1147=0的两根为a、b,且a>b,则3a+b之值为何?( )
| A、22 | B、28 | C、34 | D、40 |
如果a的相反数是-3,那么a的值是( )
| A、-3 | B、3或-3 | C、3 | D、0 |

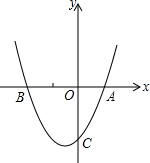 已知二次函数y=ax2+bx+c(a>0)的图象与x轴的一个交点为A(1,0),
已知二次函数y=ax2+bx+c(a>0)的图象与x轴的一个交点为A(1,0),
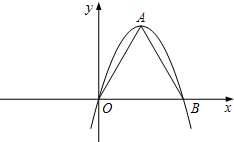 如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.
如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.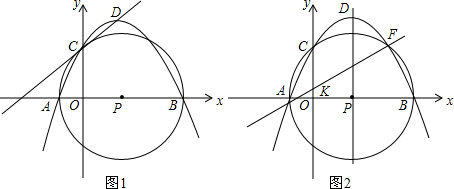
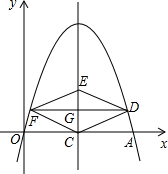 如图,在平面直角坐标系中,抛物线y=-x2+bx经过点A(4,0).直线x=2与x轴交于点C,点E是直线x=2上的一个动点,过线段CE的中点G作DF⊥CE交抛物线于D、F两点.
如图,在平面直角坐标系中,抛物线y=-x2+bx经过点A(4,0).直线x=2与x轴交于点C,点E是直线x=2上的一个动点,过线段CE的中点G作DF⊥CE交抛物线于D、F两点.