题目内容
(1)计算:(2-
)2013(2+
)2014-2|-
|-(-
)0-
÷
-
.
(2)已知关于x的不等式组
共有5个整数解,求a的取值范围.
| 3 |
| 3 |
| ||
| 2 |
| 2 |
| 8 |
| 24 |
| 27 |
(2)已知关于x的不等式组
|
考点:二次根式的混合运算,零指数幂,一元一次不等式组的整数解
专题:计算题
分析:(1)根据积的乘方与幂的乘方和零指数幂的意义得到原式=[(2-
)(2+
)]2013•(2+
)-2×
-1-
-3
,然后根据平方差公式计算后合并即可;
(2)先解不等式组得到a+3≤x<1,由于不等式组共有5个整数解,即不等式组的整数解为0,-1,-2,-3,-4,则得到关于a的不等式组-5<a+3≤-4,
然后解此不等式组即可.
| 3 |
| 3 |
| 3 |
| ||
| 2 |
| ||
| 3 |
| 3 |
(2)先解不等式组得到a+3≤x<1,由于不等式组共有5个整数解,即不等式组的整数解为0,-1,-2,-3,-4,则得到关于a的不等式组-5<a+3≤-4,
然后解此不等式组即可.
解答:解:(1)原式=[(2-
)(2+
)]2013•(2+
)-2×
-1-
-3
=2+
-
-1-
-3
=1-
;
(2)
,
解①得x<1,
解②得x≥a+3,
所以不等式组的解集为a+3≤x<1,
因为不等式组共有5个整数解,即不等式组的整数解为0,-1,-2,-3,-4,
所以-5<a+3≤-4,
解得-8<a≤-7.
| 3 |
| 3 |
| 3 |
| ||
| 2 |
| ||
| 3 |
| 3 |
=2+
| 3 |
| 3 |
| ||
| 3 |
| 3 |
=1-
10
| ||
| 3 |
(2)
|
解①得x<1,
解②得x≥a+3,
所以不等式组的解集为a+3≤x<1,
因为不等式组共有5个整数解,即不等式组的整数解为0,-1,-2,-3,-4,
所以-5<a+3≤-4,
解得-8<a≤-7.
点评:本题考查了二次根式的混合运算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.也考查了零指数幂和一元一次不等式组的整数解.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
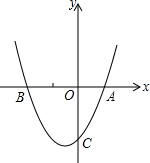 已知二次函数y=ax2+bx+c(a>0)的图象与x轴的一个交点为A(1,0),
已知二次函数y=ax2+bx+c(a>0)的图象与x轴的一个交点为A(1,0),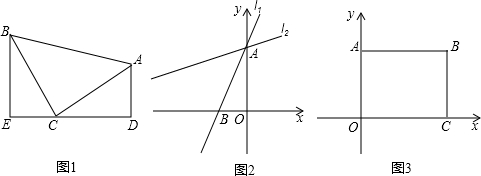
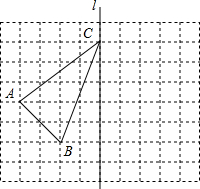 如图,在方格纸中,每个小正方形的边长为1,有一个格点△ABC(即三角形的顶点都在格点上),点C在直线l上.
如图,在方格纸中,每个小正方形的边长为1,有一个格点△ABC(即三角形的顶点都在格点上),点C在直线l上.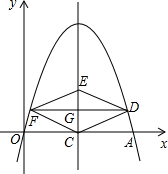 如图,在平面直角坐标系中,抛物线y=-x2+bx经过点A(4,0).直线x=2与x轴交于点C,点E是直线x=2上的一个动点,过线段CE的中点G作DF⊥CE交抛物线于D、F两点.
如图,在平面直角坐标系中,抛物线y=-x2+bx经过点A(4,0).直线x=2与x轴交于点C,点E是直线x=2上的一个动点,过线段CE的中点G作DF⊥CE交抛物线于D、F两点. 如图,△ABC中,∠C=90°,AC=
如图,△ABC中,∠C=90°,AC=