题目内容
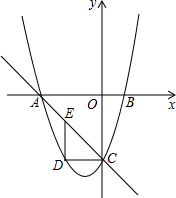 已知抛物线与x轴交于A(-3,0)、B(1,0)两点,交y轴于点C(0,-3),点E为直线AC上的一动点,DE∥y轴交抛物线于点D.
已知抛物线与x轴交于A(-3,0)、B(1,0)两点,交y轴于点C(0,-3),点E为直线AC上的一动点,DE∥y轴交抛物线于点D.(1)求抛物线y=ax2+bx+c的表达式;
(2)当点E的坐标为(-2,-1),连接AD,点P在x轴上,使△APC与△ADC相似,请求出点P的坐标;
(3)当点E在直线AC上运动时,是否存在以D、E、O、C为顶点,OC为一边的平行四边形?若存在请直接写出点E的坐标;若不存在,请说明理由.
考点:二次函数综合题
专题:
分析:(1)由于抛物线与x轴交于A(-3,0)、B(1,0)两点,交y轴于点C(0,-3),根据待定系数法即可得到抛物线y=ax2+bx+c的表达式;
(2)由图可知△ADC与△CPA相似,P点只能在A点右侧,分两种情况:若△ADC∽△CPA;若△ADC∽△PCA;进行讨论即可得到点P的坐标;
(3)根据待定系数法可得直线AC的解析式,再分两种情况:DE在y轴的右边和DE在y轴的左边;进行讨论即可得到点E的坐标.
(2)由图可知△ADC与△CPA相似,P点只能在A点右侧,分两种情况:若△ADC∽△CPA;若△ADC∽△PCA;进行讨论即可得到点P的坐标;
(3)根据待定系数法可得直线AC的解析式,再分两种情况:DE在y轴的右边和DE在y轴的左边;进行讨论即可得到点E的坐标.
解答:解:(1)∵抛物线与x轴交于A(-3,0)、B(1,0)两点,交y轴于点C(0,-3),
∴
,
解得
.
∴抛物线y=ax2+bx+c的表达式为y=x2+2x-3;
(2)∵E(-2,-1)且DE∥y轴,
∴点D与点E的横坐标相同为-2,
将x=-2代入抛物线解析式中得:y=-3
∴D(-2,-3)
又∵C(0,-3)
∴DC∥x轴且DC=2
∴∠BAC=∠ACD,
又∵A(-3,0),C(0,-3),
∴OA=OC=3,
∴AC=
=3
由图可知△ADC与△CPA相似,P点只能在A点右侧,
若△ADC∽△CPA,则
=
即
=1,
解得:AP=2,
∴P(-1,0)
若△ADC∽△PCA,则
=
即
=
,
解得:AP=9,
∴P(6,0).
∴点P的坐标为(-1,0)或(6,0);
(3)答:存在满足条件的E点.
设直线AC的解析式为y=kx+b,则
解得
.
故直线AC的解析式为y=-x-3.
设点E的坐标为(m,-m-3),则点D的坐标为(m,m2+2m-3),
当DE在y轴的右边时,m2+2m-3-(-m-3)=3,解得m1=
,m2=
(不合题意舍去),
则-m-3=
,
则E1(
,
);
当DE在y轴的左边时,m2+2m-3-(-m-3)=3,解得m1=
(不合题意舍去),m2=
,
则-m-3=
,
则E2(
,
);
综上所述,点E的坐标E1(
,
),E2(
,
).
∴
|
解得
|
∴抛物线y=ax2+bx+c的表达式为y=x2+2x-3;
(2)∵E(-2,-1)且DE∥y轴,
∴点D与点E的横坐标相同为-2,
将x=-2代入抛物线解析式中得:y=-3
∴D(-2,-3)
又∵C(0,-3)
∴DC∥x轴且DC=2
∴∠BAC=∠ACD,
又∵A(-3,0),C(0,-3),
∴OA=OC=3,
∴AC=
| 32+32 |
| 2 |
由图可知△ADC与△CPA相似,P点只能在A点右侧,
若△ADC∽△CPA,则
| CD |
| AP |
| CA |
| AC |
| 2 |
| AP |
解得:AP=2,
∴P(-1,0)
若△ADC∽△PCA,则
| CD |
| CA |
| AC |
| AP |
| 2 | ||
3
|
3
| ||
| AP |
解得:AP=9,
∴P(6,0).
∴点P的坐标为(-1,0)或(6,0);
(3)答:存在满足条件的E点.
设直线AC的解析式为y=kx+b,则
|
解得
|
故直线AC的解析式为y=-x-3.
设点E的坐标为(m,-m-3),则点D的坐标为(m,m2+2m-3),
当DE在y轴的右边时,m2+2m-3-(-m-3)=3,解得m1=
-3+
| ||
| 2 |
-3-
| ||
| 2 |
则-m-3=
-3-
| ||
| 2 |
则E1(
-3+
| ||
| 2 |
-3-
| ||
| 2 |
当DE在y轴的左边时,m2+2m-3-(-m-3)=3,解得m1=
-3+
| ||
| 2 |
-3-
| ||
| 2 |
则-m-3=
-3+
| ||
| 2 |
则E2(
-3-
| ||
| 2 |
-3+
| ||
| 2 |
综上所述,点E的坐标E1(
-3+
| ||
| 2 |
-3-
| ||
| 2 |
-3-
| ||
| 2 |
-3+
| ||
| 2 |
点评:考查了二次函数综合题,涉及的知识点有:待定系数法求抛物线的表达式,待定系数法求直线的表达式,相似三角形的性质,勾股定理,两点间的距离公式,分类思想的运用,综合性较强,有一定的难度.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
要组织一次篮球联赛,赛制为单循环形式(每两队之间都赛一场),计划安排21场比赛.设参赛球队的个数为x,则根据题意所列的方程是( )
| A、x(x+1)=21 |
| B、x(x-1)=21 |
| C、x(x+1)=21×2 |
| D、x(x-1)=21×2 |
一次函数y=kx+b中,y随x的增大而增大,b<0,则这个函数的图象不经过( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
 如图,小丽从O点出发,先向西走20米,再向北走30米到达点M,如果点M的位置用(-20,30)表示,那么(20,-30)表示的位置是( )
如图,小丽从O点出发,先向西走20米,再向北走30米到达点M,如果点M的位置用(-20,30)表示,那么(20,-30)表示的位置是( )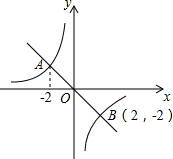 如图,在平面直角坐标系xOy中,一次函数y1=kx的图象与反比例函数y2=
如图,在平面直角坐标系xOy中,一次函数y1=kx的图象与反比例函数y2=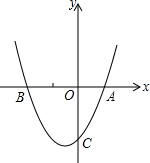 已知二次函数y=ax2+bx+c(a>0)的图象与x轴的一个交点为A(1,0),
已知二次函数y=ax2+bx+c(a>0)的图象与x轴的一个交点为A(1,0), 如图,已知∠ABC=180°-∠A,BD⊥CD于D,EF⊥CD于F.
如图,已知∠ABC=180°-∠A,BD⊥CD于D,EF⊥CD于F.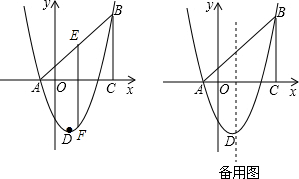
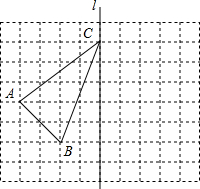 如图,在方格纸中,每个小正方形的边长为1,有一个格点△ABC(即三角形的顶点都在格点上),点C在直线l上.
如图,在方格纸中,每个小正方形的边长为1,有一个格点△ABC(即三角形的顶点都在格点上),点C在直线l上.