题目内容
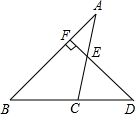 如图,已知D为△ABC边BC延长线上一点,DF⊥AB于F交AC于E,∠A=30°,∠D=55°,求∠ACD的度数.
如图,已知D为△ABC边BC延长线上一点,DF⊥AB于F交AC于E,∠A=30°,∠D=55°,求∠ACD的度数.考点:三角形内角和定理,三角形的外角性质
专题:
分析:根据三角形外角与内角的关系及三角形内角和定理解答.
解答:解:∵DF⊥AB
∴∠AFE=90°,
∴∠AEF=90°-∠A=90°-30°=60°,
∴∠CED=∠AEF=60°,
∴∠ACD=180°-∠CED-∠D=180°-60°-55°=65°.
答:∠ACD的度数为65°.
∴∠AFE=90°,
∴∠AEF=90°-∠A=90°-30°=60°,
∴∠CED=∠AEF=60°,
∴∠ACD=180°-∠CED-∠D=180°-60°-55°=65°.
答:∠ACD的度数为65°.
点评:此题考查三角形外角与内角的关系:三角形的一个外角等于和它不相邻的两个内角的和.三角形内角和定理:三角形的三个内角和为180°.

练习册系列答案
 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
 由两个相同的正方体和一个圆锥体组成一个立体图形,如果从上向下看到的平面图形是( )
由两个相同的正方体和一个圆锥体组成一个立体图形,如果从上向下看到的平面图形是( )



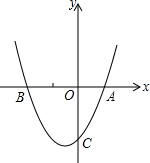 已知二次函数y=ax2+bx+c(a>0)的图象与x轴的一个交点为A(1,0),
已知二次函数y=ax2+bx+c(a>0)的图象与x轴的一个交点为A(1,0),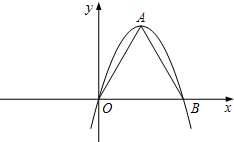 如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.
如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.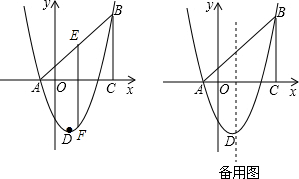
 如图,△ABC中,∠C=90°,AC=
如图,△ABC中,∠C=90°,AC=