题目内容
分式方程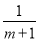 =
=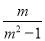 的最简公分母是__________
的最简公分母是__________
 【解析】式子,所以最简公分母是.故答案为: .
【解析】式子,所以最简公分母是.故答案为: .
练习册系列答案
相关题目
求下列各式的值.
(1)已知xa=2,xb=6,x≠0,求x3a-2b的值;
(2)若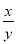 = -2,求
= -2,求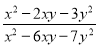 的值.
的值.
 (1) ;(2) .
【解析】试题分析: 根据同底数幂的除法和幂的乘方进行运算即可.
将进行变形,代入所求式子进行运算即可.
试题解析:
原式
(1) ;(2) .
【解析】试题分析: 根据同底数幂的除法和幂的乘方进行运算即可.
将进行变形,代入所求式子进行运算即可.
试题解析:
原式 如图,已知AB∥CD,BE⊥AD,垂足为点E,CF⊥AD,垂足为点F,并且AE=DF. 求证:四边形BECF是平行四边形.
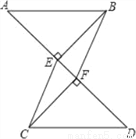
 见解析
【解析】试题分析:通过全等三角形(△AEB≌△DFC)的对应边相等证得BE=CF,由“在同一平面内,同垂直于同一条直线的两条直线相互平行”证得BE∥CF.则四边形BECF是平行四边形.
证明:∵BE⊥AD,CF⊥AD,
∴∠AEB=∠DFC=90°,
∵AB∥CD,
∴∠A=∠D,
在△AEB与△DFC中,
,
∴△AEB≌△DFC(ASA)...
见解析
【解析】试题分析:通过全等三角形(△AEB≌△DFC)的对应边相等证得BE=CF,由“在同一平面内,同垂直于同一条直线的两条直线相互平行”证得BE∥CF.则四边形BECF是平行四边形.
证明:∵BE⊥AD,CF⊥AD,
∴∠AEB=∠DFC=90°,
∵AB∥CD,
∴∠A=∠D,
在△AEB与△DFC中,
,
∴△AEB≌△DFC(ASA)... 如图,在平行四边形ABCD中,AD=5,AB=3,AE平分∠BAD交BC边于点E,则线段BE,EC的长度分别为( )
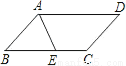
A. 2和3 B. 3和2 C. 4和1 D. 1和4
 A
【解析】试题分析:∵AE平分∠BAD交BC边于点E,∴∠BAE=∠EAD,∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC=5,∴∠DAE=∠AEB,∴∠BAE=∠AEB,∴AB=BE=3,
∴EC=BC﹣BE=5﹣3=2,故选B.
A
【解析】试题分析:∵AE平分∠BAD交BC边于点E,∴∠BAE=∠EAD,∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC=5,∴∠DAE=∠AEB,∴∠BAE=∠AEB,∴AB=BE=3,
∴EC=BC﹣BE=5﹣3=2,故选B. 解方程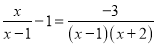
 【解析】分析:观察可得最简公分母是(x-1)(x+2),方程两边乘最简公分母,可以把分式方程转化为整式方程求解;
本题解析:两边同时乘最简公分母
化成整式方程为:
整理得到: ,经检验是方程的解.
【解析】分析:观察可得最简公分母是(x-1)(x+2),方程两边乘最简公分母,可以把分式方程转化为整式方程求解;
本题解析:两边同时乘最简公分母
化成整式方程为:
整理得到: ,经检验是方程的解. 若分式方程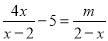 无解,那么
无解,那么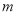 的值应为___________.
的值应为___________.
 -8
【解析】试题解析: 分式方程无解,
把原方程去分母得:
把代入方程,得
故答案为:
-8
【解析】试题解析: 分式方程无解,
把原方程去分母得:
把代入方程,得
故答案为: 解方程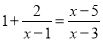 时,去分母得( )
时,去分母得( )
A. 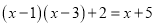 B.
B. 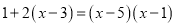
C. 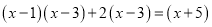 D.
D. 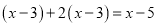
 C
【解析】观察可得最简公分母是(x-1)(x-3),方程两边都乘最简公分母,即可把分式方程转换为整式方程.
方程两边同乘(x-1)(x-3)得(x-1)(x-3)+2(x-3)=(x-5)(x-1),
故选C.
C
【解析】观察可得最简公分母是(x-1)(x-3),方程两边都乘最简公分母,即可把分式方程转换为整式方程.
方程两边同乘(x-1)(x-3)得(x-1)(x-3)+2(x-3)=(x-5)(x-1),
故选C. 若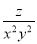 +M=
+M=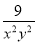 ,则M为( )
,则M为( )
A. 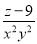 B.
B. 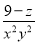 C.
C. 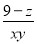 D.
D. 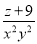
 B
【解析】∵+M=,
∴M=.
故选B.
B
【解析】∵+M=,
∴M=.
故选B. 在△ABC中,AB=AC,BD是角平分线,BD=AD,求∠A的度数.
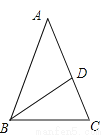
 ∠A=36°
【解析】试题分析:设∠A的度数为x°,由等腰三角形的性质分别表示出∠ABC和∠C的度数,再根据三角形内角和列方程求解即可.
试题解析:
设∠A=x°,
∵BD=AD,
∴∠A=∠ABD=x°,
∴∠BDC=∠A+∠ABD=2x°,
∵BD=BC,
∴∠BDC=∠BCD=2x°,
∵AB=AC,
∴∠ABC=∠BCD=2x°,...
∠A=36°
【解析】试题分析:设∠A的度数为x°,由等腰三角形的性质分别表示出∠ABC和∠C的度数,再根据三角形内角和列方程求解即可.
试题解析:
设∠A=x°,
∵BD=AD,
∴∠A=∠ABD=x°,
∴∠BDC=∠A+∠ABD=2x°,
∵BD=BC,
∴∠BDC=∠BCD=2x°,
∵AB=AC,
∴∠ABC=∠BCD=2x°,... 
