题目内容
已知在等边△ABC中,D、E、F、G、H、L是三边的三等分点.求证:六边形DEFGHL是正六边形.
考点:正多边形和圆,等边三角形的性质
专题:证明题
分析:先由等边三角形的性质得出∠A=∠B=∠C=60°,AB=BC=AC=a,再根据三等分点的意义可得AD=DE=BE=BF=FG=GC=CH=HL=AL=
a,由AD=AL及∠A=60°判定△ADL是等边三角形,那么DL=AD=AL=
a,∠ADL=∠ALD=60°,进而得出六边形DEFGHL的各条边都相等,各个角也相等,从而判定六边形DEFGHL是正六边形.
| 1 |
| 3 |
| 1 |
| 3 |
解答: 证明:设△ABC的边长为a.
证明:设△ABC的边长为a.
如图,∵△ABC是等边三角形,
∴∠A=∠B=∠C=60°,AB=BC=AC=a,
∵D、E、F、G、H、L是三边的三等分点,
∴AD=DE=BE=BF=FG=GC=CH=HL=AL=
a,
∴△ADL是等边三角形,
∴DL=AD=AL=
a,∠ADL=∠ALD=60°,
同理EF=GH═
a,∠BEF=∠BFE=60°,∠CGH=∠CHG=60°,
∴DL=DE=EF=FG=GH=HL=
a;∠LDE=∠DEF=∠EFG=∠FGH=∠GHL=∠HLD=180°-60°=120°,
∴六边形DEFGHL是正六边形.
 证明:设△ABC的边长为a.
证明:设△ABC的边长为a.如图,∵△ABC是等边三角形,
∴∠A=∠B=∠C=60°,AB=BC=AC=a,
∵D、E、F、G、H、L是三边的三等分点,
∴AD=DE=BE=BF=FG=GC=CH=HL=AL=
| 1 |
| 3 |
∴△ADL是等边三角形,
∴DL=AD=AL=
| 1 |
| 3 |
同理EF=GH═
| 1 |
| 3 |
∴DL=DE=EF=FG=GH=HL=
| 1 |
| 3 |
∴六边形DEFGHL是正六边形.
点评:本题考查了等边三角形的判定与性质,正六边形的判定,难度适中.掌握正六边形的定义是解题的关键.

练习册系列答案
相关题目
 如图所示,它是小孔成像的原理,根据图中尺寸(AB∥CD),如果已知物体AB=30,则CD的长应是( )
如图所示,它是小孔成像的原理,根据图中尺寸(AB∥CD),如果已知物体AB=30,则CD的长应是( )| A、15 | B、30 | C、20 | D、10 |
小明和小亮口袋里面都放有五张不同的北京奥运会福娃纪念卡,则两人分别在自己口袋里摸出一张福娃都是欢欢的概率是( )


A、
| ||
B、
| ||
C、
| ||
| D、1 |
 如图,小正方体的棱长为1,求对角线AG的长.
如图,小正方体的棱长为1,求对角线AG的长.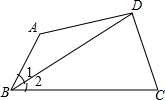 如图,BC>AB,∠1=∠2,AD=CD,探究∠BAD与∠C的关系.(用三种方法解答)
如图,BC>AB,∠1=∠2,AD=CD,探究∠BAD与∠C的关系.(用三种方法解答) 如图所示,已知∠ABC=∠ADC=90°,AC与BD相交于点P,点E,F分别是AC,BD的中点,判断△EFP的形状.
如图所示,已知∠ABC=∠ADC=90°,AC与BD相交于点P,点E,F分别是AC,BD的中点,判断△EFP的形状.