题目内容
若分式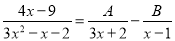 (A、B为常数),则A、B 的值为 ( )
(A、B为常数),则A、B 的值为 ( )
A. 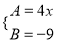 B.
B. 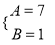 C.
C. 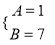 D.
D. 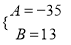
 B
【解析】= ,则 ,故选B.
B
【解析】= ,则 ,故选B.
练习册系列答案
相关题目
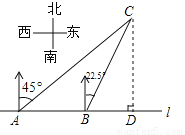
如图,在一笔直的海岸线l上有A、B两个观测站,AB=2km、从A测得船C在北偏东45°的方向,从B测得船C在北偏东22.5°的方向,则船C离海岸线l的距离(即CD的长)为( )
A. 4km B. (2+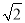 )km C. 2
)km C. 2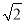 km D. (4-
km D. (4-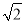 )km
)km
 B
【解析】试题分析:根据题意中方位角的特点,过点B作BE⊥AC,交AC于点E,由∠CAB=45°,AB=2km,可知BE=km,根据题意还可知∠BCA=∠BCD=22.5°,因此CB是∠ACD的角平分线,根据角平分线的性质可得:BD=BE=km,因此CD=AD=AB+BD=(2+)km,故选B.
B
【解析】试题分析:根据题意中方位角的特点,过点B作BE⊥AC,交AC于点E,由∠CAB=45°,AB=2km,可知BE=km,根据题意还可知∠BCA=∠BCD=22.5°,因此CB是∠ACD的角平分线,根据角平分线的性质可得:BD=BE=km,因此CD=AD=AB+BD=(2+)km,故选B. 在多边形的内角中,锐角的个数不能多于( )
A. 2个 B. 3个 C. 4个 D. 5个
 B
【解析】多边形的外角和是360°,因此外角中最多有三个钝角,外角与相邻的内角互为邻补角,
所以在多边形的内角中,锐角的个数不能多于3个,
故选B.
B
【解析】多边形的外角和是360°,因此外角中最多有三个钝角,外角与相邻的内角互为邻补角,
所以在多边形的内角中,锐角的个数不能多于3个,
故选B. 若关于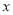 的方程
的方程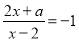 的解为正数,则
的解为正数,则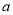 的取值范围是_____.
的取值范围是_____.
 且
【解析】解方程得: ,因为它的解是正数,则 ,得且.
故答案: 且.
且
【解析】解方程得: ,因为它的解是正数,则 ,得且.
故答案: 且. 若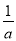 +
+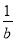 =
=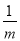 (a≠b≠0),用含a、b的代数式表示m,则m=___________.
(a≠b≠0),用含a、b的代数式表示m,则m=___________.
 【解析】根据+=得, ,得: .
故答案: .
【解析】根据+=得, ,得: .
故答案: . 下列关于x的方程是分式方程的是( )
A. 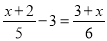 ; B.
; B. 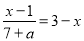 ; C.
; C. 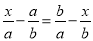 ; D.
; D. 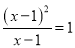
 D
【解析】根据分式方程的定义——分母中含有未知数的方程.故选D.
D
【解析】根据分式方程的定义——分母中含有未知数的方程.故选D. 若对于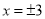 以外的一切数
以外的一切数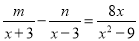 均成立,则
均成立,则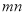 的值是( )
的值是( )
A. 8 B. 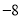 C. 16 D.
C. 16 D. 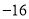
 D
【解析】,则 ,得: .
故选D.
D
【解析】,则 ,得: .
故选D. 化简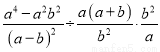 的结果是( )
的结果是( )
A. 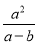 B.
B. 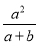 C.
C. 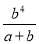 D.
D. 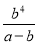
 D
【解析】试题解析:原式
故选D.
D
【解析】试题解析:原式
故选D. 如图所示,在?ABCD中,对角线AC,BD相交于点O,E,F是对角线AC上的两点,当E,F满足下列哪个条件时,四边形DEBF不一定是平行四边形( )
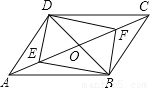
A.OE=OF B.DE=BF C.∠ADE=∠CBF D.∠ABE=∠CDF
 B.
【解析】
试题分析:A、∵四边形ABCD是平行四边形,∴OD=OB,又∵OE=OF,∴四边形DEBF是平行四边形.能判定是平行四边形.B、DE=BF,OD=OB,缺少夹角相等.不能利用全等判断出OE=OF,∴DE=BF,∴四边形DEBF不一定是平行四边形.C、D均能证明四边形DEBF是平行四边形.
故选:B.
B.
【解析】
试题分析:A、∵四边形ABCD是平行四边形,∴OD=OB,又∵OE=OF,∴四边形DEBF是平行四边形.能判定是平行四边形.B、DE=BF,OD=OB,缺少夹角相等.不能利用全等判断出OE=OF,∴DE=BF,∴四边形DEBF不一定是平行四边形.C、D均能证明四边形DEBF是平行四边形.
故选:B.