题目内容
2．在△ABC中，∠C=90°，a、b分别是∠A、∠B的对边，a2-ab-b2=0，则tanA=（ ）| A． | $\frac{{1+\sqrt{5}}}{2}$ | B． | $\frac{{1-\sqrt{5}}}{2}$ | C． | $\frac{{1±\sqrt{5}}}{2}$ | D． | 1 |
分析 把a2-ab-b2=0看作关于a的一元二次方程，利用求根公式法解方程得到$\frac{a}{b}$=$\frac{1+\sqrt{5}}{2}$，然后利用正切的定义求解．
解答 解：△=（-b）2-4×（-b2）=5b2，
a=$\frac{b±\sqrt{5}b}{2}$
所以a1=$\frac{1+\sqrt{5}}{2}$b，a2=$\frac{1-\sqrt{5}}{2}$b（舍去），
∴$\frac{a}{b}$=$\frac{1+\sqrt{5}}{2}$，
∴tanA=$\frac{a}{b}$=$\frac{1+\sqrt{5}}{2}$．
故选A．
点评 本题考查了解一元二次方程-公式法：用求根公式解一元二次方程的方法是公式法．
练习册系列答案
相关题目
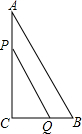如图，△ABC中，∠C=90°，BC=5厘米，AB=5$\sqrt{5}$厘米，点P从点A出发沿AC边以2厘米/秒的速度向终点C匀速移动，同时，点Q从点C出发沿CB边以1厘米/秒的速度向终点B匀速移动，P、Q两点运动几秒时，P、Q两点间的距离是2$\sqrt{10}$厘米？
10．
如图，在平面直角坐标系中，⊙P的圆心是（2，a），半径为2，直线y=-x与⊙P相交于A、B两点，若弦AB的长为2$\sqrt{3}$，则a的值是（ ）
如图，在平面直角坐标系中，⊙P的圆心是（2，a），半径为2，直线y=-x与⊙P相交于A、B两点，若弦AB的长为2$\sqrt{3}$，则a的值是（ ）| A． | -2$\sqrt{2}$ | B． | -2+$\sqrt{2}$ | C． | -2-$\sqrt{3}$ | D． | -2-$\sqrt{2}$ |
17．
如图，直线y=$\frac{4}{3}$x-4与x轴、y轴分别交于A、B两点，把△AOB以x轴为对称轴翻折得到△AOB′，再将△AOB′绕点A顺时针旋转90°，得到△AO′B″，则点B″的坐标是（ ）
如图，直线y=$\frac{4}{3}$x-4与x轴、y轴分别交于A、B两点，把△AOB以x轴为对称轴翻折得到△AOB′，再将△AOB′绕点A顺时针旋转90°，得到△AO′B″，则点B″的坐标是（ ）| A． | （3，4） | B． | （4，4） | C． | （7，3） | D． | （7，4） |
（1）阅读理解：
如图，正六边形ABCDEF，连结AC，求作点P，Q使它们成为AC的三等分点，下列作法正确的是（ ）
如图所示，在△ABE和△ACD中，给出以下4个论断：