题目内容
7. (1)阅读理解:
(1)阅读理解:我们知道,只用直尺和圆规不能解决的三个经典的希腊问题之一是三等分任意角,但是这个任务可以借助如图所示的一边上有刻度的勾尺完成,勾尺的直角顶点为P,“宽臂”的宽度=PQ=QR=RS,(这个条件很重要哦!)勾尺的一边MN满足M,N,Q三点共线(所以PQ⊥MN).
下面以三等分∠ABC为例说明利用勾尺三等分锐角的过程:
第一步:画直线DE使DE∥BC,且这两条平行线的距离等于PQ;
第二步:移动勾尺到合适位置,使其顶点P落在DE上,使勾尺的MN边经过点B,同时让点R落在∠ABC的BA边上;
第三步:标记此时点Q和点P所在位置,作射线BQ和射线BP.
请完成第三步操作,图中∠ABC的三等分线是射线BQ、BP.
(2)在(1)的条件下补全三等分∠ABC的主要证明过程:
∵PQ=QR,BQ⊥PR,
∴BP=BR.线段垂直平分线上的点到线段两个端点距离相等
∴∠RBQ=∠PBQ.
∵PQ⊥MN,PT⊥BC,PT=PQ,
∴∠PBQ=∠PBT.
(角的内部到角的两边距离相等的点在角的平分线上)
∴∠RBQ=∠QBP=∠PBT.
(3)在(1)的条件下探究:
∠ABS=$\frac{1}{3}$∠ABC是否成立?如果成立,请说明理由;如果不成立,请在下图中∠ABC的外部画出∠ABV=$\frac{1}{3}$∠ABC(无需写画法,保留画图痕迹即可).
分析 (1)作射线BQ和射线BP,射线BQ和射线BP就是∠ABC的三等分线.
(2)根据线段的垂直平分线的性质定理,等腰三角形的三线合一,角平分线的判定定理,即可证明.
(3)等式不成立.如图作点Q关于直线AB的对称点V,连接BS,∠VBA=∠ABQ=$\frac{1}{3}$∠ABC.
解答 解:(1)如图作射线BQ和射线BP,射线BQ和射线BP就是∠ABC的三等分线,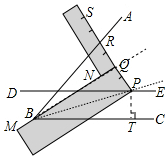
故答案为BQ、BP.
(2)∵PQ=QR,BQ⊥PR,
∴BP=BR(线段垂直平分线上的点到线段两个端点距离相等),
∴∠RBQ=∠PBQ.
∵PQ⊥MN,PT⊥BC,PT=PQ,
∴∠PBQ=∠PBT.
(角的内部到角的两边距离相等的点在角的平分线上)
∴∠RBQ=∠QBP=∠PBT,
故答案分别为线段垂直平分线上的点到线段两个端点距离相等,RBQ,QBP,PBT.
(3)等式不成立.
如图作点Q关于直线AB的对称点V,连接BS,∠VBA=∠ABQ=$\frac{1}{3}$∠ABC.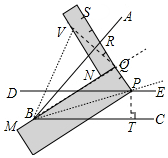
点评 本题考查三角形综合题、线段的垂直平分线的性质、角平分线的性质定理、轴对称等知识,解题的关键是理解题意,灵活运用所学知识解决问题,学会利用轴对称构造角相等,属于中考常考题型.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
2.在△ABC中,∠C=90°,a、b分别是∠A、∠B的对边,a2-ab-b2=0,则tanA=( )
| A. | $\frac{{1+\sqrt{5}}}{2}$ | B. | $\frac{{1-\sqrt{5}}}{2}$ | C. | $\frac{{1±\sqrt{5}}}{2}$ | D. | 1 |
12. 在我市开展的“美丽山城,创卫我同行”活动中,某校倡议八年级学生利用双休日在各自社区参加义务劳动.为了解同学们劳动情况,学校随机调查了部分同学的劳动时间,并用得到的数据绘制成不完整的统计图表,如图所示:
在我市开展的“美丽山城,创卫我同行”活动中,某校倡议八年级学生利用双休日在各自社区参加义务劳动.为了解同学们劳动情况,学校随机调查了部分同学的劳动时间,并用得到的数据绘制成不完整的统计图表,如图所示:
(1)统计表中的m=100,x=40,y=0.18;
(2)请将统计图补充完整;
(3)请你估计如果有2000名学生参加义务劳动时间超过1小时的人数.
 在我市开展的“美丽山城,创卫我同行”活动中,某校倡议八年级学生利用双休日在各自社区参加义务劳动.为了解同学们劳动情况,学校随机调查了部分同学的劳动时间,并用得到的数据绘制成不完整的统计图表,如图所示:
在我市开展的“美丽山城,创卫我同行”活动中,某校倡议八年级学生利用双休日在各自社区参加义务劳动.为了解同学们劳动情况,学校随机调查了部分同学的劳动时间,并用得到的数据绘制成不完整的统计图表,如图所示:| 劳动时间(时) | 频数(人数) | 频率 |
| 0.5 | 12 | 0.12 |
| 1 | 30 | 0.3 |
| 1.5 | x | 0.4 |
| 2 | 18 | y |
| 合计 | m | 1 |
(2)请将统计图补充完整;
(3)请你估计如果有2000名学生参加义务劳动时间超过1小时的人数.
 如图△ABC中,∠ACB=90°,AC+BC=8,分别以AB、AC、BC为半径作半圆,若记图中阴影部分的面积为y,AC为x,则下列y关于x的图象中正确的是( )
如图△ABC中,∠ACB=90°,AC+BC=8,分别以AB、AC、BC为半径作半圆,若记图中阴影部分的面积为y,AC为x,则下列y关于x的图象中正确的是( )



 小明同学在学习了全等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以作出一个锐角的平分线.如图:一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”你认为小明的想法正确吗?请说明理由.
小明同学在学习了全等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以作出一个锐角的平分线.如图:一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”你认为小明的想法正确吗?请说明理由. 如图,等腰三角形ABC的底边BC长为4,面积是12,腰AB的垂直平分线EF分别交AB,AC于点E、F,若点D为底边BC的中点,点M为线段EF上一动点,则△BDM的周长的最小值为8.
如图,等腰三角形ABC的底边BC长为4,面积是12,腰AB的垂直平分线EF分别交AB,AC于点E、F,若点D为底边BC的中点,点M为线段EF上一动点,则△BDM的周长的最小值为8. 如图,将100张长为30cm、宽相等的长方形白纸,按如图所示的方法粘起来,粘合的部分宽为3cm,求粘合后总长度.
如图,将100张长为30cm、宽相等的长方形白纸,按如图所示的方法粘起来,粘合的部分宽为3cm,求粘合后总长度.