Question

12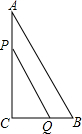．如图，△ABC中，∠C=90°，BC=5厘米，AB=5$\sqrt{5}$厘米，点P从点A出发沿AC边以2厘米/秒的速度向终点C匀速移动，同时，点Q从点C出发沿CB边以1厘米/秒的速度向终点B匀速移动，P、Q两点运动几秒时，P、Q两点间的距离是2$\sqrt{10}$厘米？

Answer 1

分析 首先表示出PC和CQ的长，然后利用勾股定理列出有关时间t的方程求解即可．

解答 解：设P、Q两点运动x秒时，P、Q两点间的距离是2$\sqrt{10}$厘米．
在△ABC中，∠C=90°，BC=5厘米，AB=5$\sqrt{5}$厘米，
∴AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=$\sqrt{（5\sqrt{5}）^{2}-{5}^{2}}$=10（厘米），
∴AP=2x 厘米    CQ=x厘米    CP=（10-2x）厘米，
在Rt△CPQ内有PC²+CQ²=PQ²，
∴（10-2x）²+x²=（2$\sqrt{10}$）²，
整理得：x²-8x+12=0，
解得：x=2或x=6，
当x=6时 CP=10-2x=-2＜0，∴x=6不合题意舍去．
∴P、Q两点运动2秒时，P、Q两点间的距离是2$\sqrt{10}$厘米．

点评 本题考查了一元二次方程的解法和应用，解决第二题的关键是设出运动时间并用运动时间表示出有关线段的长．