题目内容
14. 如图,正六边形ABCDEF,连结AC,求作点P,Q使它们成为AC的三等分点,下列作法正确的是( )
如图,正六边形ABCDEF,连结AC,求作点P,Q使它们成为AC的三等分点,下列作法正确的是( )①取AB,BC的中点M,N,再分别以A,C为圆心,以AM,CN的长为半径画弧,交AC于点P,Q
②连结 BF,BD,分别交AC于点P,Q
③连结BE交AC于点H,分别取AH,CH的中点P,Q
④作AB,BC的中垂线分别交AC于点P,Q.
| A. | ①② | B. | ②③ | C. | ②④ | D. | ③④ |
分析 如图1,连结 BF,BD,分别交AC于点P,Q,根据等腰三角形的性质得到∠BCP=∠CBP=30°,∠ABQ=∠BAQ=30°,求得PB=PC,QB=QA,∠BPQ=∠BQP=60°,于是得到结论如图2,根据线段垂直平分线的性质得到PB=PC,QB=QA,根据三角形的外角的性质得到∠BPQ=∠BQP=60°,得到PB=BQ=PQ,等量代换得到结论.
解答 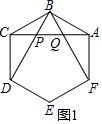 解:如图1,连结 BF,BD,分别交AC于点P,Q,
解:如图1,连结 BF,BD,分别交AC于点P,Q,
∴∠BCP=∠CBP=30°,∠ABQ=∠BAQ=30°,
∴PB=PC,QB=QA,∠BPQ=∠BQP=60°,
∴PB=BQ,
∴CP=PQ=AQ,
∴②正确;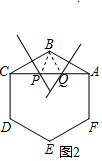
如图2,∵作AB,BC的中垂线分别交AC于点P,Q.
∴PB=PC,QB=QA,
∴∠BCP=∠CBP=∠BAQ=∠ABQ=30°,
∴∠BPQ=∠BQP=60°,
∴△BPQ是等边三角形,
∴PB=BQ=PQ,
∴CP=PQ=QA,
∴④正确.
故选C.
点评 本题考查了作图-复杂作图,正多边形的性质,等腰三角形的性质,正确的作出图形是解题的关键.

练习册系列答案
相关题目
5.相似三角形的概念是( )
| A. | 对应角相等、对应边成比例的两个三角形 | |
| B. | 两角分别相等的两个三角形 | |
| C. | 三边对应成比例的两个三角形 | |
| D. | 两边对应成比例且夹角相等的两个三角形 |
2.在△ABC中,∠C=90°,a、b分别是∠A、∠B的对边,a2-ab-b2=0,则tanA=( )
| A. | $\frac{{1+\sqrt{5}}}{2}$ | B. | $\frac{{1-\sqrt{5}}}{2}$ | C. | $\frac{{1±\sqrt{5}}}{2}$ | D. | 1 |
4. 如图,A、D是⊙O上的两个点,BC是直径,若∠ADC=33°,则∠ACB等于( )
如图,A、D是⊙O上的两个点,BC是直径,若∠ADC=33°,则∠ACB等于( )
 如图,A、D是⊙O上的两个点,BC是直径,若∠ADC=33°,则∠ACB等于( )
如图,A、D是⊙O上的两个点,BC是直径,若∠ADC=33°,则∠ACB等于( )| A. | 57° | B. | 66° | C. | 67° | D. | 44° |
 如图,⊙C过原点,与x轴、y轴分别交于A、D两点,已知cos∠ABO=$\frac{\sqrt{3}}{2}$,⊙C半径是2,则OD的长为2$\sqrt{3}$.
如图,⊙C过原点,与x轴、y轴分别交于A、D两点,已知cos∠ABO=$\frac{\sqrt{3}}{2}$,⊙C半径是2,则OD的长为2$\sqrt{3}$. Rt△ABC中∠C=90°,AC=4,cosB=$\frac{3}{5}$,半径为r的⊙C与△ABC的边有两个交点,则r的取值范围是0<r<2.4.
Rt△ABC中∠C=90°,AC=4,cosB=$\frac{3}{5}$,半径为r的⊙C与△ABC的边有两个交点,则r的取值范围是0<r<2.4. 如图,等腰三角形ABC的底边BC长为4,面积是12,腰AB的垂直平分线EF分别交AB,AC于点E、F,若点D为底边BC的中点,点M为线段EF上一动点,则△BDM的周长的最小值为8.
如图,等腰三角形ABC的底边BC长为4,面积是12,腰AB的垂直平分线EF分别交AB,AC于点E、F,若点D为底边BC的中点,点M为线段EF上一动点,则△BDM的周长的最小值为8. (1)已知⊙O的直径为6,圆心O到直线l的距离为5,
(1)已知⊙O的直径为6,圆心O到直线l的距离为5,