题目内容
3.若a,b互为相反数c,d互为倒数,m的绝对值为2,则(a+b)(a-b)+(1+2m+m2)÷(cd)-3=9或1.分析 根据a、b互为相反数且均不为0,可得:a+b=0;c、d互为倒数,可得:cd=1;m的绝对值为2,可得:m=±2;据此求出(a+b)(a-b)+(1+2m+m2)÷(cd)-3的值是多少即可.
解答 解:∵a、b互为相反数且均不为0,
∴a+b=0,$\frac{b}{a}$=-1;
∵c、d互为倒数,
∴cd=1;
∵m的绝对值为2,
∴m=±2;
(1)m=2时,
(a+b)(a-b)+(1+2m+m2)÷(cd)-3
=0+(1+2×2+4)÷1
=9
(2)m=-2时,
(a+b)(a-b)+(1+2m+m2)÷(cd)-3
=0+(1-2×2+4)÷1
=1
∴(a+b)(a-b)+(1+2m+m2)÷(cd)-3=9或1.
故答案为:9或1.
点评 此题主要考查了代数式求值问题,以及负整数指数幂的求法,要熟练掌握,求代数式的值可以直接代入、计算.如果给出的代数式可以化简,要先化简再求值.题型简单总结以下三种:①已知条件不化简,所给代数式化简;②已知条件化简,所给代数式不化简;③已知条件和所给代数式都要化简.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.已知一个正数的两个平方根分别为2a-5和1-a,则这个正数为( )
| A. | 3 | B. | 4 | C. | 9 | D. | 16 |
12.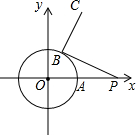 在平面直角坐标系中,以原点O为圆心的圆过点A(2,0),B点为⊙O上任意一点,P(5,0),连接BP,将线段BP绕B点逆时针旋转90°至线段BC,当B点从A点出发,绕圆旋转一周的过程中,C点运动路径长为( )
在平面直角坐标系中,以原点O为圆心的圆过点A(2,0),B点为⊙O上任意一点,P(5,0),连接BP,将线段BP绕B点逆时针旋转90°至线段BC,当B点从A点出发,绕圆旋转一周的过程中,C点运动路径长为( )
 在平面直角坐标系中,以原点O为圆心的圆过点A(2,0),B点为⊙O上任意一点,P(5,0),连接BP,将线段BP绕B点逆时针旋转90°至线段BC,当B点从A点出发,绕圆旋转一周的过程中,C点运动路径长为( )
在平面直角坐标系中,以原点O为圆心的圆过点A(2,0),B点为⊙O上任意一点,P(5,0),连接BP,将线段BP绕B点逆时针旋转90°至线段BC,当B点从A点出发,绕圆旋转一周的过程中,C点运动路径长为( )| A. | 2$\sqrt{2}$π | B. | 4π | C. | 4$\sqrt{2}$π | D. | 6π |
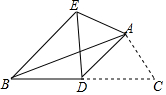 如图,已知AD是△ABC的中线,∠ADC=45°,把△ADC沿AD所在直线对折,点C落在点E的位置,求∠EBC的度数.
如图,已知AD是△ABC的中线,∠ADC=45°,把△ADC沿AD所在直线对折,点C落在点E的位置,求∠EBC的度数.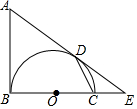 如图,AB是以BC为直径的半圆O的切线,D为半圆上一点,AD=AB,AD、BC的延长线相交于点E.
如图,AB是以BC为直径的半圆O的切线,D为半圆上一点,AD=AB,AD、BC的延长线相交于点E.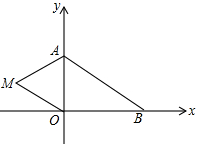 如图,在平面直角坐标系中,已知A(0,a),B(b,0),其中a,b满足|a-2|+(b-3)2=0.
如图,在平面直角坐标系中,已知A(0,a),B(b,0),其中a,b满足|a-2|+(b-3)2=0.