题目内容
10．下列四组数，可作为直角三角形三边长的是（ ）| A． | 5cm、12cm、13cm | B． | 1cm、2cm、3cm | C． | 2cm、3cm、4cm | D． | 4cm、5cm、6cm |
分析 欲求证是否为直角三角形，这里给出三边的长，只要验证两小边的平方和等于最长边的平方即可．
解答 解：A、52+122=132，故能构成直角三角形；
B、12+22≠32，故不能构成直角三角形；
C、22+32≠42，故不能构成直角三角形；
D、52+42≠62，故不能构成直角三角形．
故选A．
点评 本题考查勾股定理的逆定理的应用．判断三角形是否为直角三角形，已知三角形三边的长，只要利用勾股定理的逆定理加以判断即可．勾股定理的逆定理：若三角形三边满足a2+b2=c2，那么这个三角形是直角三角形．
练习册系列答案
黄冈小状元解决问题天天练系列答案
三点一测快乐周计划系列答案
相关题目
13．下列各式是最简二次根式的是（ ）
| A． | $\sqrt{12}$ | B． | $\sqrt{3x}$ | C． | $\sqrt{{2x}^{3}}$ | D． | $\sqrt{\frac{5}{3}}$ |
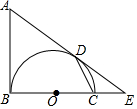如图，AB是以BC为直径的半圆O的切线，D为半圆上一点，AD=AB，AD、BC的延长线相交于点E．
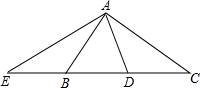如图，AD是直角三角形ABC斜边上的中线，AE⊥AD交CB延长线于E，则图中一定相似的三角形是C说明理由．
19．
如图，△ABC内接于⊙O，⊙O的半径为5，sin∠B=$\frac{3}{5}$，点D在边AC上，在弧BC上取一点E．使得∠CDE=∠ABC．且AE=$\sqrt{3}$DE．则CD的长为（ ）
如图，△ABC内接于⊙O，⊙O的半径为5，sin∠B=$\frac{3}{5}$，点D在边AC上，在弧BC上取一点E．使得∠CDE=∠ABC．且AE=$\sqrt{3}$DE．则CD的长为（ ）| A． | 2$\sqrt{2}$ | B． | 2 | C． | $\sqrt{3}$ | D． | 2.5 |
某人沿坡度为1：3的斜坡从坡底A处行走至坡顶B处，已知AB=3$\sqrt{10}$米，在B处测得AD延长线上一物体C的俯角α为37°，求坡底A到物体C的距离．