题目内容
18.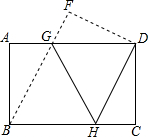 将矩形纸片ABCD如图折叠,使点B与点D重合,折痕为GH.
将矩形纸片ABCD如图折叠,使点B与点D重合,折痕为GH.(1)试说明:AG=GF;
(2)试说明:四边形DGBH是菱形;
(1)若AB=12,BC=16.求GH的长.
分析 (1)欲证明AG=GF,只要证明ABG≌△FDG即可.
(2)先证明四边形DGBH是平行四边形,再证明是菱形.
(3)作GE⊥BC于E,设AG=x,则DG=BG=16-x,在RT△ABG中利用勾股定理求出x,再在RT△GHE中利用勾股定理即可解决问题.
解答 (1)证明:∵四边形ABCD是矩形,GH是折痕,
∴∠A=∠F=90°,AB=DF
在△ABG和△FDG中,
$\left\{\begin{array}{l}{∠A=∠F}\\{∠AGB=∠FGD}\\{AB=DF}\end{array}\right.$,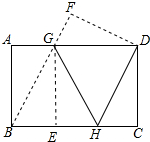
∴△ABG≌△FDG,
∴AG=GF.
(2)证明:由折叠知BH=DH,∠BHG=∠DHG,
∵AD∥BC,
∴∠DGH=∠BHG,
∴∠DHG=∠DGH,
∴DG=DH,
∵DG平行且等于BH,
∴四边形DGBH为平行四边形,
∵BH=DH,
∴四边形DGBH是菱形.
(3)解:作GE⊥BC于E,设AG=x,则DG=BG=16-x,
在RT△ABG中,AB2+AG2=BG2,列方程得:122+x2=(16-x)2,
解得:x=3.5,
∴BE=AG=3.5,HE=BH-BE=12.5-3.5=9,
在RT△GHE中,∵GH2=GE2+EH2=122+92=225,
∴GH=15.
点评 本题考查翻折变换、全等三角形的判定和性质、勾股定理等知识,解题的关键是熟练掌握全等三角形的判定方法以及菱形的判定方法,学会转化的思想,用方程的思想思考问题,属于中考常考题型.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
4.已知一个多边形的内角和等于它的外角和的2倍,则这个多边形的边数为( )
| A. | 8 | B. | 7 | C. | 6 | D. | 5 |
7. 如图,已知直线CD∥AB,若∠DFE=130°,则∠ABE的度数为( )
如图,已知直线CD∥AB,若∠DFE=130°,则∠ABE的度数为( )
 如图,已知直线CD∥AB,若∠DFE=130°,则∠ABE的度数为( )
如图,已知直线CD∥AB,若∠DFE=130°,则∠ABE的度数为( )| A. | 30° | B. | 50° | C. | 60° | D. | 130° |
8. 将直尺和直角三角板按如图位置摆放,若∠1=25°,则∠2的度数是( )
将直尺和直角三角板按如图位置摆放,若∠1=25°,则∠2的度数是( )
 将直尺和直角三角板按如图位置摆放,若∠1=25°,则∠2的度数是( )
将直尺和直角三角板按如图位置摆放,若∠1=25°,则∠2的度数是( )| A. | 35° | B. | 45° | C. | 55° | D. | 65° |
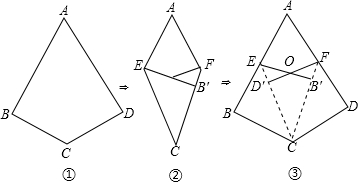
 如图,图①是棱长为4cm的立方体,沿其相邻三个面的对角线(虚线)裁掉一个角,得到如图②的几何体,则一只蚂蚁沿着图②几何体的表面,从顶点A爬到顶点B的最短距离为(2$\sqrt{2}$+2$\sqrt{6}$)cm.
如图,图①是棱长为4cm的立方体,沿其相邻三个面的对角线(虚线)裁掉一个角,得到如图②的几何体,则一只蚂蚁沿着图②几何体的表面,从顶点A爬到顶点B的最短距离为(2$\sqrt{2}$+2$\sqrt{6}$)cm.