题目内容
11.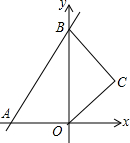 如图,直线y=x+2于x、y轴分别交于点A、B两点,以OB为边在y轴右侧作等边三角形OBC,将点C向左平移,使其对应点C′恰好落在直线AB上,则点C移动的距离为$\sqrt{3}$+1.
如图,直线y=x+2于x、y轴分别交于点A、B两点,以OB为边在y轴右侧作等边三角形OBC,将点C向左平移,使其对应点C′恰好落在直线AB上,则点C移动的距离为$\sqrt{3}$+1.
分析 先求出直线y=x+2与y轴交点B的坐标为(0,2),再由C在线段OB的垂直平分线上,得出C点纵坐标为1,将y=1代入y=x+2,求得x=-1,即可得到C′的坐标为(-1,1),进而得出点C移动的距离.
解答 解:∵直线y=x+2与y轴交于B点,
∴x=0时,
得y=2,
∴B(0,2).
∵以OB为边在y轴右侧作等边三角形OBC,
∴C在线段OB的垂直平分线上,
∴C点纵坐标为1.
将y=1代入y=x+2,得1=x+2,
解得x=-1.
故C点到y轴的距离为:$\sqrt{3}$,故点C移动的距离为:$\sqrt{3}$+1.
故答案为:$\sqrt{3}$+1.
点评 本题考查了一次函数图象上点的坐标特征,等边三角形的性质,坐标与图形变化-平移,得出C点纵坐标为1是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.若代数式$\frac{1}{2}(a-1)$的值不大于-1,则a的取值范围是( )
| A. | a≤2 | B. | a≤-1 | C. | a≤-2 | D. | a≥-3 |
 如图所示,P是等边三角形ABC内一点,且∠APB:∠BPC:∠CPA=3:4:5,求以PA,PB,PC为边的三角形的三个内角的度数.
如图所示,P是等边三角形ABC内一点,且∠APB:∠BPC:∠CPA=3:4:5,求以PA,PB,PC为边的三角形的三个内角的度数.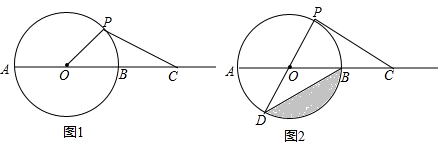
 如图,将矩形ABCD沿直线CE折叠,顶点B恰好落在AD边上F点处,若CD=8,BE=5,则FD的长为( )
如图,将矩形ABCD沿直线CE折叠,顶点B恰好落在AD边上F点处,若CD=8,BE=5,则FD的长为( ) 如图,一块铁片边缘是由抛物线和线段AB组成,测得AB=20cm,抛物线的顶点到AB边的距离为25cm.现要沿AB边向上依次截取宽度均为4cm的矩形铁皮,从下往上依次是第一块,第二块…如图所示.已知截得的铁皮中有一块是正方形,则这块正方形铁皮是第6块.
如图,一块铁片边缘是由抛物线和线段AB组成,测得AB=20cm,抛物线的顶点到AB边的距离为25cm.现要沿AB边向上依次截取宽度均为4cm的矩形铁皮,从下往上依次是第一块,第二块…如图所示.已知截得的铁皮中有一块是正方形,则这块正方形铁皮是第6块.