题目内容
20. 如图,网格中的每个小正方形的边长为1,A,B是格点,则以A,B,C为等腰三角形顶点的所有格点C的位置有( )
如图,网格中的每个小正方形的边长为1,A,B是格点,则以A,B,C为等腰三角形顶点的所有格点C的位置有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
分析 由勾股定理求出AB=$\sqrt{{3}^{2}+{1}^{2}}$=$\sqrt{10}$,分三种情况讨论:①当A为顶角顶点时;②当B为顶角顶点时;③当C为顶角顶点时;即可得出结果.
解答 解: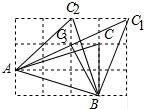 由勾股定理得:AB=$\sqrt{{3}^{2}+{1}^{2}}$=$\sqrt{10}$,
由勾股定理得:AB=$\sqrt{{3}^{2}+{1}^{2}}$=$\sqrt{10}$,
分三种情况:如图所示:
①当A为顶角顶点时,符合△ABC为等腰三角形的C点有1个;
②当B为顶角顶点时,符合△ABC为等腰三角形的C点有2个;
③当C为顶角顶点时,符合△ABC为等腰三角形的C点有1个;
综上所述:以A,B,C为等腰三角形顶点的所有格点C的位置有1+2+1=4(个);
故选:C.
点评 本题考查了等腰三角形的判定、勾股定理、正方形的性质;熟练掌握等腰三角形的判定,分情况讨论是解决问题的关键.

练习册系列答案
相关题目
11.已知,AB是⊙O的一条弦,∠AOB=120°,则AB所对的圆周角为( )
| A. | 60° | B. | 90° | C. | 120° | D. | 60°或120° |
15.下列结论正确的是( )
| A. | $\sqrt{(-2)^{2}}$=-2 | B. | $\root{3}{(-2)^{3}}$=-2 | C. | $\sqrt{(±2)^{2}}$=±2 | D. | $\root{3}{{2}^{3}}$=±2 |
9.已知等腰△ABC的两边长分别为2cm和3cm,则△ABC的周长为( )
| A. | 7cm | B. | 8cm | C. | 6cm或8cm | D. | 7cm或8cm |




 如图,AB是⊙O的直径,点C是AB延长线上一点,CD是⊙O的切线,点D是切点,过点B作⊙O的切线,交CD于点E,若CD=8,BE=3,则⊙O的半径为( )
如图,AB是⊙O的直径,点C是AB延长线上一点,CD是⊙O的切线,点D是切点,过点B作⊙O的切线,交CD于点E,若CD=8,BE=3,则⊙O的半径为( ) 如图,已知在△ABC中,∠A=90°
如图,已知在△ABC中,∠A=90° 如图,把矩形纸片ABCD沿对角线AC折叠,点B落在点E处,P、Q分别是AD、EC的中点,PQ交AE、CD于点M、N,若AB=4,AD=3,求线段MN的长.
如图,把矩形纸片ABCD沿对角线AC折叠,点B落在点E处,P、Q分别是AD、EC的中点,PQ交AE、CD于点M、N,若AB=4,AD=3,求线段MN的长.