题目内容
5. 如图,已知在△ABC中,∠A=90°
如图,已知在△ABC中,∠A=90°(1)请用圆规和直尺作出⊙P,使圆心P在AC边上,且与AB,BC两边都相切(保留作图痕迹,不写作法和证明).
(2)若⊙P与BC的切点为D,∠B=60°,AB=3,求劣弧$\widehat{AD}$的长.
分析 (1)作∠ABC的角平分线BE,交AC与P,再以P为圆心,AP长为半径画圆即可;
(2)连接PD,根据四边形内角和为360°可得∠APD=120°,根据角平分线的定义可得∠ABP=30°,然后再根据三角函数tan∠ABP=$\frac{AP}{AB}$,可得AP长,再利用弧长公式可得答案.
解答  解:(1)如图所示:
解:(1)如图所示:
(2)连接PD,
∵∠B=60°,BP平分∠ABC,
∴∠ABP=30°,∠APD=120°,
∵tan∠ABP=$\frac{AP}{AB}$,
∴AP=$\sqrt{3}$,
∴劣弧$\widehat{AD}$的长为$\frac{120π•\sqrt{3}}{180}$=$\frac{2\sqrt{3}π}{3}$.
点评 此题主要考查了复杂作图以及弧长计算,关键是掌握弧长公式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.以下事件为必然事件的是( )
| A. | 掷一枚质地均匀的骰子,向上一面的点数小于6 | |
| B. | 多边形的内角和是360° | |
| C. | 二次函数的图象不过原点 | |
| D. | 半径为2的圆的周长是4π |
16.甲、乙两地相距270千米,从甲地开出一辆快车,速度为120千米/时,从乙地开出一辆慢车,速度为75千米/时,如果两车相向而行,慢车先开出1小时后,快车开出,那么再经过多长时间两车相遇?若设再经过x小时两车相遇,则根据题意列方程为( )
| A. | 75×1+(120-75)x=270 | B. | 75×1+(120+75)x=270 | ||
| C. | 120(x-1)+75x=270 | D. | 120×1+(120+75)x=270 |
20. 如图,网格中的每个小正方形的边长为1,A,B是格点,则以A,B,C为等腰三角形顶点的所有格点C的位置有( )
如图,网格中的每个小正方形的边长为1,A,B是格点,则以A,B,C为等腰三角形顶点的所有格点C的位置有( )
 如图,网格中的每个小正方形的边长为1,A,B是格点,则以A,B,C为等腰三角形顶点的所有格点C的位置有( )
如图,网格中的每个小正方形的边长为1,A,B是格点,则以A,B,C为等腰三角形顶点的所有格点C的位置有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
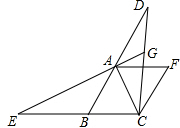 如图,在?ABCF中,∠ABC=60°,AB=BC,延长BA到D,延长CB到E,使BE=AD,连结DC,交AF于H,连结EA并延长交CD于点G.
如图,在?ABCF中,∠ABC=60°,AB=BC,延长BA到D,延长CB到E,使BE=AD,连结DC,交AF于H,连结EA并延长交CD于点G. 如图,矩形ABCD中,点B与原点重合,点D(8,6),AE⊥BD,△AEB沿着y轴翻折得到△AFB,将△AFB绕着点B顺时针旋转α(0°<α<90°)得到△BF′A′,直线F′A′与线段AB、AE分别交于点M、N,当MN=MA时,△BF′A′与△AEB重叠部分的面积为$\frac{108}{25}$.
如图,矩形ABCD中,点B与原点重合,点D(8,6),AE⊥BD,△AEB沿着y轴翻折得到△AFB,将△AFB绕着点B顺时针旋转α(0°<α<90°)得到△BF′A′,直线F′A′与线段AB、AE分别交于点M、N,当MN=MA时,△BF′A′与△AEB重叠部分的面积为$\frac{108}{25}$.