题目内容
5. 如图,把矩形纸片ABCD沿对角线AC折叠,点B落在点E处,P、Q分别是AD、EC的中点,PQ交AE、CD于点M、N,若AB=4,AD=3,求线段MN的长.
如图,把矩形纸片ABCD沿对角线AC折叠,点B落在点E处,P、Q分别是AD、EC的中点,PQ交AE、CD于点M、N,若AB=4,AD=3,求线段MN的长.
分析 如图首先根据条件证明DE∥AC,再证明AM∥HN,得四边形MNHA是平行四边形,利用面积法求出高DH,利用勾股定理求出AH,根据MN=AH可以解决问题.
解答 解:(1)∵四边形ABCD为矩形,AD=3,AB=4,
∴AD=BC=3,AB=DC=4,CD∥AB,∠B=90°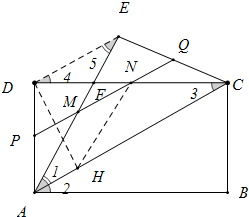
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=5cm,∠2=∠3,
∵将矩形ABCD沿对角线AC折叠,使点B落在点E处,
∴∠1=∠2,
∴∠1=∠3,
∴AF=CF,∵AE=CD,
∴DF=EF,
∴∠4=∠5,
∴∠1=∠5=∠4=∠3,
∴DE∥AC,
∵AD=CE=3cm,且AD与CE不平行,
∴四边形ACED是等腰梯形,
过点D、E分别作DH⊥AC于点H,
在Rt△ACD中,$\frac{1}{2}$DH•AC=$\frac{1}{2}$AD•DC,则DH=$\frac{12}{5}$,在Rt△ADH中,AH=$\sqrt{A{D}^{2}-D{H}^{2}}$=$\frac{9}{5}$,
∵DE∥AC,DP=AP,EQ=QC
∴DE∥PQ∥AC,DN=NC,
∵∠DHC=90°,
∴HN=NC=DN,
∴∠3=∠NHC=∠1,
∴NH∥AM,
∵MN∥AH,
∴四边形MNHA是平行四边形,
∴MN=AH=$\frac{9}{5}$.
点评 本题主要考查的是翻折的性质、等腰三角形的性质和判定、平行四边形的判定和性质、勾股定理、面积法的应用,由翻折的性质找出相等的角或边是解题的关键.

练习册系列答案
相关题目
20. 如图,网格中的每个小正方形的边长为1,A,B是格点,则以A,B,C为等腰三角形顶点的所有格点C的位置有( )
如图,网格中的每个小正方形的边长为1,A,B是格点,则以A,B,C为等腰三角形顶点的所有格点C的位置有( )
 如图,网格中的每个小正方形的边长为1,A,B是格点,则以A,B,C为等腰三角形顶点的所有格点C的位置有( )
如图,网格中的每个小正方形的边长为1,A,B是格点,则以A,B,C为等腰三角形顶点的所有格点C的位置有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
1. 如图,在△ABC中,∠ACB=90°,BE平分∠ABC,DE⊥AB于D,如果AC=3cm,那么AE+DE等于( )
如图,在△ABC中,∠ACB=90°,BE平分∠ABC,DE⊥AB于D,如果AC=3cm,那么AE+DE等于( )
 如图,在△ABC中,∠ACB=90°,BE平分∠ABC,DE⊥AB于D,如果AC=3cm,那么AE+DE等于( )
如图,在△ABC中,∠ACB=90°,BE平分∠ABC,DE⊥AB于D,如果AC=3cm,那么AE+DE等于( )| A. | 2cm | B. | 3cm | C. | 4cm | D. | 5cm |
14.下列运算正确的是( )
| A. | (-x3)2=x6 | B. | 3x+2y=6xy | C. | x2•x4=x6 | D. | y3÷y3=y |
 如图,一建筑物AB(看做线段)在阳光下的投影为BC,小红站在BC上,现她不想看到自己的影子,请你在图上画出她的活动范围.
如图,一建筑物AB(看做线段)在阳光下的投影为BC,小红站在BC上,现她不想看到自己的影子,请你在图上画出她的活动范围. 如图,矩形ABCD中,点B与原点重合,点D(8,6),AE⊥BD,△AEB沿着y轴翻折得到△AFB,将△AFB绕着点B顺时针旋转α(0°<α<90°)得到△BF′A′,直线F′A′与线段AB、AE分别交于点M、N,当MN=MA时,△BF′A′与△AEB重叠部分的面积为$\frac{108}{25}$.
如图,矩形ABCD中,点B与原点重合,点D(8,6),AE⊥BD,△AEB沿着y轴翻折得到△AFB,将△AFB绕着点B顺时针旋转α(0°<α<90°)得到△BF′A′,直线F′A′与线段AB、AE分别交于点M、N,当MN=MA时,△BF′A′与△AEB重叠部分的面积为$\frac{108}{25}$. 在平面直角坐标系中,已知点B的坐标是(-1,0),点A的坐标是(4,0),点C的坐标是(0,4),抛物线过A、B、C三点.
在平面直角坐标系中,已知点B的坐标是(-1,0),点A的坐标是(4,0),点C的坐标是(0,4),抛物线过A、B、C三点. 反比例函数y=$\frac{k}{x}$的图象如图所示,点M是该函数图象上一点,MN垂直于x轴,垂足是点N,如果S△MON=3,那么k的值是-6.
反比例函数y=$\frac{k}{x}$的图象如图所示,点M是该函数图象上一点,MN垂直于x轴,垂足是点N,如果S△MON=3,那么k的值是-6.