题目内容
12.m条直线两两相交,最多有10个交点,则列得的方程是( )| A. | 2m=10 | B. | m+(m-1)=10 | C. | $\frac{m(m-1)}{2}$=10 | D. | m(m-1)=10 |
分析 根据m条直线的交点最多有$\frac{m(m-1)}{2}$个,根据题意可得方程$\frac{m(m-1)}{2}$=10.
解答 解:由题意得:$\frac{m(m-1)}{2}$=10.
故选:C.
点评 此题主要考查了由实际问题抽象出一元二次方程,关键是掌握m条直线两两相交,交点个数最多的计算公式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.下列说法正确的是( )
| A. | 若a>0,b>0,则$\frac{a}{b}$>0 | B. | 若$\frac{a}{b}$>0,则a<0,b<0, | ||
| C. | 若a•b=0,则a=0且b=0 | D. | 若a•b>0,则a>0,b>0 |
20. 如图,平行四边形ABCD的对角线BD的长为4cm,将平行四边形ABCD绕其对角线的交点O旋转180°,则点B所经过的路径长为( )
如图,平行四边形ABCD的对角线BD的长为4cm,将平行四边形ABCD绕其对角线的交点O旋转180°,则点B所经过的路径长为( )
 如图,平行四边形ABCD的对角线BD的长为4cm,将平行四边形ABCD绕其对角线的交点O旋转180°,则点B所经过的路径长为( )
如图,平行四边形ABCD的对角线BD的长为4cm,将平行四边形ABCD绕其对角线的交点O旋转180°,则点B所经过的路径长为( )| A. | 4πcm | B. | 3πcm | C. | 2πcm | D. | πcm |
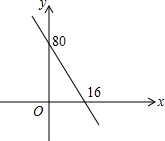 某汽车销售公司销售某种型号的汽车,每辆车进价6万元,售价为x万元,经市场调查发现销售量y与销售价x的关系如图.
某汽车销售公司销售某种型号的汽车,每辆车进价6万元,售价为x万元,经市场调查发现销售量y与销售价x的关系如图.