题目内容
7.Rt△ABC中,∠C=90°,∠B的平分线交AC于E,DE⊥BE.试说明AC是△BED外接圆的切线.分析 根据圆周角定理即可证得BD是外接圆的直径,则作出BD的中点就是圆的圆心,连接OE,证明OE⊥AC即可证得AC是切线.
解答  证明:作BD的中点O,连接OE.
证明:作BD的中点O,连接OE.
∵DE⊥BE,
∴BD是△BED外接圆的直径.
∵OB=OE,
∴∠EBO=∠BEO,
又∵∠CBE=∠EBO,
在直角△BCE中,∠CBE+∠CEB=90°,
∴∠CBE+∠BEO=90°,即∠CEO=90°.
∴OE⊥AC,
∴AC是△BED外接圆的切线.
点评 本题考查了圆的切线的判定,以及圆周角定理,正确作出辅助线,证明OE⊥AC是关键.

练习册系列答案
相关题目
15.迄今为止,科学家发现了约76万种昆虫,这张表表示昆虫的主要类群种数.利用这些数据,绘制一张扇形图,来表示每种昆虫所占的百分比.
| 种群 | 蚂蚁、蜜蜂和黄蜂 | 甲虫、象鼻虫 | 蝴蝶、蛾 | 苍蝇、蚊子 | 其他昆虫 |
| 种数/万 | 10 | 30 | 11 | 10 | 15 |
12.m条直线两两相交,最多有10个交点,则列得的方程是( )
| A. | 2m=10 | B. | m+(m-1)=10 | C. | $\frac{m(m-1)}{2}$=10 | D. | m(m-1)=10 |
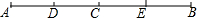 如图,已知点C是线段AB的中点,点D是线段AC的中点,点E是线段BC的中点.
如图,已知点C是线段AB的中点,点D是线段AC的中点,点E是线段BC的中点.