题目内容
6. 如图,在?ABCD中,AB=6,AD=8,∠ADC的平分线交BC于点F,交AB的延长线于点G,过点C作CE⊥DG,垂足为E,CE=2,则△BFG的周长为4+$\frac{8\sqrt{2}}{3}$.
如图,在?ABCD中,AB=6,AD=8,∠ADC的平分线交BC于点F,交AB的延长线于点G,过点C作CE⊥DG,垂足为E,CE=2,则△BFG的周长为4+$\frac{8\sqrt{2}}{3}$.
分析 首先利用已知条件可证明△ADE是等腰三角形,根据等腰三角形“三线合一”的性质得出DE=2DG,而在Rt△ADG中,由勾股定理可求得DG的值,即可求得DE的长;然后,证明△ADE∽△BFE,再分别求出△ADE的周长,然后根据周长比等于相似比即可得到答案.
解答 解:∵DE平分∠ADC,
∴∠ADE=∠CDE;,
又∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠ADE=∠CDF=∠DFC,
∴CD=CF=6,
∵CE⊥DG,
∴DF=2DE,
在Rt△CDE中,∵∠DEC=90°,CD=6,CE=2,
∴DE=$\sqrt{C{D}^{2}-C{E}^{2}}$=4$\sqrt{2}$,
∴DF=2DE=8$\sqrt{2}$;
∴△CDF的周长=12+8$\sqrt{2}$,
∵CF=6,BC=AD=8,
∴BF=BC-CF=8-6=2,
∴CF:BF=6:2=3:1.
∵AB∥CD,
∴△CDF∽△BFG,
∴△CDF的周长:△BFG的周长=CF:BF=3:1,
则△BFG 周长=4+$\frac{8\sqrt{2}}{3}$.
故答案为:4+$\frac{8\sqrt{2}}{3}$.
点评 本题考查了平行四边形的性质,相似三角形的判定与性质,勾股定理等知识的掌握程度和灵活运用能力,同时也体现了对数学中的数形结合思想的考查,难度适中.

练习册系列答案
相关题目
17.下列计算正确的是( )
| A. | 3a+2b=5ab | B. | (a+2b)2=a2+4b2 | C. | a2•a3=a5 | D. | 4x2y-2xy2=2xy |
1.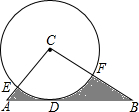 如图,在Rt△ABC中,∠C=90°,∠B=30°,以点C为圆心,4为半径的⊙C与AB相切于点D,交CA于E,交CB于F,则图中阴影部分的面积为( )
如图,在Rt△ABC中,∠C=90°,∠B=30°,以点C为圆心,4为半径的⊙C与AB相切于点D,交CA于E,交CB于F,则图中阴影部分的面积为( )
 如图,在Rt△ABC中,∠C=90°,∠B=30°,以点C为圆心,4为半径的⊙C与AB相切于点D,交CA于E,交CB于F,则图中阴影部分的面积为( )
如图,在Rt△ABC中,∠C=90°,∠B=30°,以点C为圆心,4为半径的⊙C与AB相切于点D,交CA于E,交CB于F,则图中阴影部分的面积为( )| A. | $\frac{32}{3}\sqrt{3}-4π$ | B. | $\frac{32}{3}\sqrt{3}-2π$ | C. | 16-4π | D. | 16-2π |
18.方程x2-5x=0的解是( )
| A. | x1=x2=5 | B. | x1=x2=0 | C. | x1=0,x2=5 | D. | x1=-5,x2=0 |
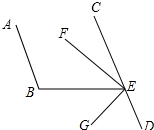 如图,已知AB∥CD,∠B=96°,EF平分∠BEC,EG⊥EF,求∠BEG和∠DEG的度数.
如图,已知AB∥CD,∠B=96°,EF平分∠BEC,EG⊥EF,求∠BEG和∠DEG的度数.
 平面上,将边长相等的正三角形、正方形、正六边形的一边重合并叠在一起,如图,则∠1+∠2+∠3=60°.
平面上,将边长相等的正三角形、正方形、正六边形的一边重合并叠在一起,如图,则∠1+∠2+∠3=60°. 已知:△ABC
已知:△ABC