Question

16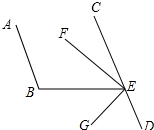．如图，已知AB∥CD，∠B=96°，EF平分∠BEC，EG⊥EF，求∠BEG和∠DEG的度数．

Answer 1

分析 首先根据平行线的性质可得∠B+∠CEB=180°，进而可得∠CEB的度数，再根据角平分线的定义可得∠FEB的度数，然后再根据垂直定义可得∠GEB的度数；利用邻补角的性质可得∠BED，再根据角的和差关系可得∠DEG的度数．

解答 解：∵AB∥CD，
∴∠B+∠CEB=180°，
∵∠B=96°，
∴∠CEB=180°-96°=84°，
∵EF平分∠BEC，
∴∠BEF=84°÷2=42°，
∵EG⊥EF，
∴∠FEG=90°，
∴∠BEG=90°-42°=48°，
∵∠CEB=84°，
∴∠BED=96°，
∴∠DEG=96°-48°=48°．

点评 此题主要考查了平行线的性质，以及角平分线定义，垂直定义，关键是掌握两直线平行，同旁内角互补．