题目内容
3. 如图,在△ABC中,点Q,M在BC上,点P,N分别在AB,AC上,边BC=120毫米,高AD=80毫米,四边形PQMN为矩形,设△ABC的高AD与PN相交于点E.
如图,在△ABC中,点Q,M在BC上,点P,N分别在AB,AC上,边BC=120毫米,高AD=80毫米,四边形PQMN为矩形,设△ABC的高AD与PN相交于点E.(1)若这个矩形是正方形,则边长是多少?
(2)若这个矩形的长是宽的2倍,则长和宽各是多少?
分析 (1)PN与AD交于点E,设MN=xmm,则AE=AD-ED=80-x,再证明△APN∽△ABC,利用相似比可求出正方形边长;
(2)设长方形的宽为y毫米,由(1)得△APN∽△ABC,利用相似比列方程即可得到结果.
解答 解:(1)设正方形的边长为x毫米,
∵四边形PQMN为正方形,
∴PN∥QM,
∴△APN∽△ABC,
∴$\frac{PN}{BC}=\frac{AE}{AD}$,即$\frac{x}{120}=\frac{80-x}{80}$,
解得x=48,
∴正方形的边长是48mm;
(2)设长方形的宽为y毫米,由(1)得△APN∽△ABC,
∴$\frac{PN}{BC}=\frac{AE}{AD}$,即$\frac{y}{120}=\frac{80-2y}{80}$,或$\frac{2y}{120}=\frac{80-y}{80}$,
解得y=30或y=$\frac{240}{7}$,
∴长方形的宽为30mm,长为60mm或宽为$\frac{240}{7}$ mm,长为$\frac{480}{7}$ mm.
点评 本题考查了相似三角形的应用:利用相似三角形的性质即相似三角形的对应边的比相等计算线段的长.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
11.3×(-$\frac{1}{3}$)的结果是( )
| A. | -4 | B. | -1 | C. | -$\frac{1}{4}$ | D. | $\frac{3}{2}$ |
12.下列计算中,正确的是( )
| A. | $\sqrt{3}$-$\sqrt{2}$=1 | B. | $\sqrt{8}$-$\sqrt{2}$=4 | C. | 2+$\sqrt{3}$=2$\sqrt{3}$ | D. | $\frac{\sqrt{8}}{2}$=$\sqrt{2}$ |
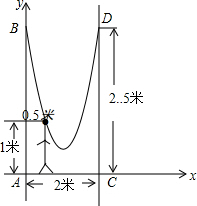 如图,小明的父亲在相距2米的两棵树(AB、CD)间拴了一根绳子,给小明做了一个简易的秋千.拴绳子的地方距地面高都是2.5米,绳子自然下垂呈抛物线状,身高1米的小明距较近的那棵树0.5米时,头部刚好接触到绳子.以A为原点,AC所在直线为x轴,AB所在直线为y轴,建立如图所示的直角坐标系.
如图,小明的父亲在相距2米的两棵树(AB、CD)间拴了一根绳子,给小明做了一个简易的秋千.拴绳子的地方距地面高都是2.5米,绳子自然下垂呈抛物线状,身高1米的小明距较近的那棵树0.5米时,头部刚好接触到绳子.以A为原点,AC所在直线为x轴,AB所在直线为y轴,建立如图所示的直角坐标系.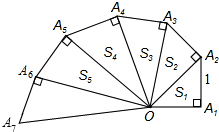 细心观察图形,认真分析各式,然后解答问题.
细心观察图形,认真分析各式,然后解答问题.