题目内容
18.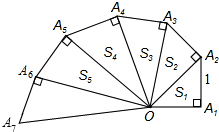 细心观察图形,认真分析各式,然后解答问题.
细心观察图形,认真分析各式,然后解答问题.($\sqrt{1}$)2+1=2 S1=$\frac{\sqrt{1}}{2}$
($\sqrt{2}$)2+1=3 S2=$\frac{\sqrt{2}}{2}$
($\sqrt{3}$)2+1=4 S3=$\frac{\sqrt{3}}{2}$
…
(1)推算出S10的值;
(2)请用含有n(n是正整数)的等式表示上述变化规律;
(3)求出S12+S22+S32+…+S102的值.
分析 (1)由给出的数据直接写出OA102的长,从而得到S10的值即可;
(2)分别求出OA12,OA22,OA33…和S1、S2、S3…Sn,找出规律即;
(3)首先求出S12+S22+S32+…+Sn2的公式,然后把n=10代入即可.
解答 解:(1)∵OA12=1,OA22=2,OA32=3,
∴OA102=10,
∵S1=$\frac{\sqrt{1}}{2}$,S2=$\frac{\sqrt{2}}{2}$,S3=$\frac{\sqrt{3}}{2}$,…
∴S10=$\frac{\sqrt{10}}{2}$;
(2)由(1)得:OAn2=n,Sn=$\frac{\sqrt{n}}{2}$;
(3)∵S12=$\frac{1}{4}$,S22=$\frac{2}{4}$,S32=$\frac{3}{4}$,…S102=$\frac{10}{4}$,
S12+S22+S32+…+Sn2=$\frac{1}{4}$+$\frac{2}{4}$+$\frac{3}{4}$+…+$\frac{10}{4}$=$\frac{55}{4}$.
点评 本题主要考查勾股定理的知识点,解答本题的关键是熟练运用勾股定理,此题难度不大.

练习册系列答案
相关题目
2.若71800000=7.18×10n,则n等于( )
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
13.已知x=-2是方程x2+bx-2=0的一个根,则方程的另一个根是( )
| A. | 1 | B. | 2 | C. | -2 | D. | -1 |
8.下列用科学记数法表示的数正确的是( )
| A. | 30×106 | B. | -14×103 | C. | 0.8×105 | D. | 4.00×106 |
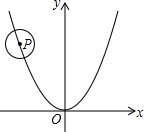 如图,已知⊙P的半径为2,圆心P在抛物线y=x2-2上运动,当⊙P与x轴相切时,圆心P的坐标为(2,2)或(-2,2).
如图,已知⊙P的半径为2,圆心P在抛物线y=x2-2上运动,当⊙P与x轴相切时,圆心P的坐标为(2,2)或(-2,2).
 如图,在△ABC中,点Q,M在BC上,点P,N分别在AB,AC上,边BC=120毫米,高AD=80毫米,四边形PQMN为矩形,设△ABC的高AD与PN相交于点E.
如图,在△ABC中,点Q,M在BC上,点P,N分别在AB,AC上,边BC=120毫米,高AD=80毫米,四边形PQMN为矩形,设△ABC的高AD与PN相交于点E.