题目内容
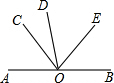 如图,A,O,B在一条直线上,AB⊥OD,且∠AOC=∠EOD.
如图,A,O,B在一条直线上,AB⊥OD,且∠AOC=∠EOD.(1)若∠BOE是它的余角的一半,求∠DOE的大小;
(2)若∠AOC:∠COB=1:2,求∠EOB的大小.
考点:余角和补角
专题:
分析:(1)根据垂线的定义,可得∠BOD的度数,根据余角的性质,可得答案;
(2)根据角的比例:∠AOC:∠COB=1:2,补角的性质,可得∠AOC的度数,根据根据余角的性质,可得答案.
(2)根据角的比例:∠AOC:∠COB=1:2,补角的性质,可得∠AOC的度数,根据根据余角的性质,可得答案.
解答:解:(1)由AB⊥OD,得
∠BOD=90°.
由∠BOE是它的余角的一半,得
∠BOE=
∠DOE,即90°-∠DOE=
∠DOE.
解得∠DOE=60°;
(2)由∠AOC:∠COB=1:2,得
∠BOC=2∠AOC.
由∠AOC+∠BOC=180°得
∠AOC=60°.
由∠AOC=∠EOD=60°,∠EOD+∠EOB=90°,得
∠EOB=90°-∠EOD=90°-60°=30°.
∠BOD=90°.
由∠BOE是它的余角的一半,得
∠BOE=
| 1 |
| 2 |
| 1 |
| 2 |
解得∠DOE=60°;
(2)由∠AOC:∠COB=1:2,得
∠BOC=2∠AOC.
由∠AOC+∠BOC=180°得
∠AOC=60°.
由∠AOC=∠EOD=60°,∠EOD+∠EOB=90°,得
∠EOB=90°-∠EOD=90°-60°=30°.
点评:本题考查了余角和补角,(1)由∠BOE是它的余角的一半,得90°-∠DOE=
∠DOE是解题关键,(2)利用了角的和差∠AOC+∠BOC=180°得∠AOC=60°.
| 1 |
| 2 |

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
下列说法正确的是( )
| A、球的截面可能是椭圆 |
| B、组成长方体的各个面中不能有正方形 |
| C、五棱柱一共有15条棱 |
| D、正方体的截面可能是七边形 |
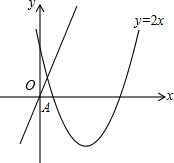 已知抛物线y=2x2+bx+6经过A(1,0),点P为抛物线的顶点,点B为抛物线与x轴的另一交点.
已知抛物线y=2x2+bx+6经过A(1,0),点P为抛物线的顶点,点B为抛物线与x轴的另一交点. 如图,已知BO,CO分别是∠ABC的外角平分线,试说明∠BOC=90°-
如图,已知BO,CO分别是∠ABC的外角平分线,试说明∠BOC=90°- 如图,长方形OABC在平面直角坐标系xOy的第一象限内,点A在x轴正半轴上,点C在y轴的正半轴上,点D、E分别是OC、BC的中点,∠CDE=30°,点E的坐标为(2,a).
如图,长方形OABC在平面直角坐标系xOy的第一象限内,点A在x轴正半轴上,点C在y轴的正半轴上,点D、E分别是OC、BC的中点,∠CDE=30°,点E的坐标为(2,a).