题目内容
 如图,已知BO,CO分别是∠ABC的外角平分线,试说明∠BOC=90°-
如图,已知BO,CO分别是∠ABC的外角平分线,试说明∠BOC=90°-| 1 |
| 2 |
考点:三角形内角和定理,三角形的外角性质
专题:
分析:如图,证明∠OBC+∠OCB=180°-
;结合α+β=180°-∠A,即可解决问题.
| α+β |
| 2 |
解答: 证明:设∠ABC、∠ACB分别为α、β;
证明:设∠ABC、∠ACB分别为α、β;
∵BO,CO分别是∠ABC、∠ACB的外角平分线,
∴∠OBC=
,∠OCB=
,
∴∠OBC+∠OCB=180°-
;
∵α+β=180°-∠A,
∴∠BOC=90°-
∠A.
 证明:设∠ABC、∠ACB分别为α、β;
证明:设∠ABC、∠ACB分别为α、β;∵BO,CO分别是∠ABC、∠ACB的外角平分线,
∴∠OBC=
| 180°-α |
| 2 |
| 180°-β |
| 2 |
∴∠OBC+∠OCB=180°-
| α+β |
| 2 |
∵α+β=180°-∠A,
∴∠BOC=90°-
| 1 |
| 2 |
点评:该题主要考查了三角形的内角和定理、外角的性质及其应用问题;解题的关键是灵活运用有关定理来分析、判断、推理或解答.

练习册系列答案
相关题目
 如图,左面的正方体展开图是( )
如图,左面的正方体展开图是( )A、 |
B、 |
C、 |
D、 |
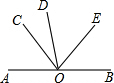 如图,A,O,B在一条直线上,AB⊥OD,且∠AOC=∠EOD.
如图,A,O,B在一条直线上,AB⊥OD,且∠AOC=∠EOD.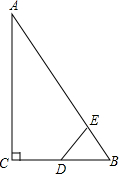 如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,D为BC的中点.若动点E以1cm/s的速度从A点出发,沿着A→B→A的方向运动,设E点的运动时间为t秒(0≤t<6),连接DE,当△BDE是直角三角形时,求t的值.
如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,D为BC的中点.若动点E以1cm/s的速度从A点出发,沿着A→B→A的方向运动,设E点的运动时间为t秒(0≤t<6),连接DE,当△BDE是直角三角形时,求t的值.