题目内容
13.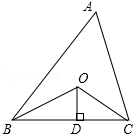 如图所示,已知△ABC的周长是20,OB、OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=3,则△ABC的面积是30.
如图所示,已知△ABC的周长是20,OB、OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=3,则△ABC的面积是30.
分析 根据角平分线上的点到角的两边的距离相等可得点O到AB、AC、BC的距离都相等(即OE=OD=OF),从而可得到△ABC的面积等于周长的一半乘以3,代入求出即可.
解答 解:如图,连接OA,过O作OE⊥AB于E,OF⊥AC于F,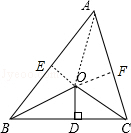
∵OB、OC分别平分∠ABC和∠ACB,
∴OE=OF=OD=3,
∵△ABC的周长是20,OD⊥BC于D,且OD=3,
∴S△ABC=$\frac{1}{2}$×AB×OE+$\frac{1}{2}$×BC×OD+$\frac{1}{2}$×AC×OF=$\frac{1}{2}$×(AB+BC+AC)×3
=$\frac{1}{2}×$20×3=30,
故答案为:30.
点评 本题考查了角平分线上的点到角的两边的距离相等的性质,判断出三角形的面积与周长的关系是解题的关键.

练习册系列答案
相关题目
1.从数轴上看,大于-3且小于2的整数有( )
| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
18.为丰富学生学习生活,学校举行绘画展,小强所绘长为80cm,宽为50cm的图画被选中去参加展览,图画四周镶上一条等宽的金边装裱成一幅矩形挂图后,图画的面积是整个挂图面积的$\frac{20}{27}$.若设金边的宽度为xcm,那么x满足的方程是( )
| A. | $(80+2x)(50+2x)×\frac{20}{27}=80×50$ | B. | $(80+2x)(50+2x)=80×50×\frac{20}{27}$ | ||
| C. | $(80-2x)(50-2x)×\frac{20}{27}=80×50$ | D. | $(80-2x)(50-2x)=80×50×\frac{20}{27}$ |
2.下列运算正确的是( )
| A. | $\sqrt{4}$=±2 | B. | ±$\sqrt{16}$=4 | C. | $\root{3}{-8}$=-2 | D. | -$\sqrt{(-3)^{2}}$=3 |
 如图,△ABC中,∠ABC=90°,AC=CE,BC=CD,∠ACE=∠BCD=90°,BC的延长线交DE于F.
如图,△ABC中,∠ABC=90°,AC=CE,BC=CD,∠ACE=∠BCD=90°,BC的延长线交DE于F.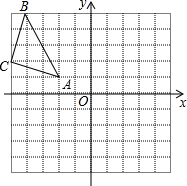 如图,△ABC在平面直角坐标系中,其中,点A、B、C的坐标分别为A(-2,1),B(-4,5),C(-5,2).
如图,△ABC在平面直角坐标系中,其中,点A、B、C的坐标分别为A(-2,1),B(-4,5),C(-5,2). 如图,∠BAD=90°,射线AC平分∠BAE.
如图,∠BAD=90°,射线AC平分∠BAE.