题目内容
3. 如图,△ABC中,∠ABC=90°,AC=CE,BC=CD,∠ACE=∠BCD=90°,BC的延长线交DE于F.
如图,△ABC中,∠ABC=90°,AC=CE,BC=CD,∠ACE=∠BCD=90°,BC的延长线交DE于F.(1)求证:EF=DF;
(2)求证:S△ABC=S△DCE.
分析 (1)作EG⊥BF,交BF延长线于G;证出∠ECG=∠BAC,由AAS证明△ABC≌△CGE,得出BC=EG,再由AAS证明△CFD≌△GFE,得出对应边相等即可;
(2)由全等三角形的性质得出面积相等S△DCE=S△CGE,S△ABC=S△CGE,即可得出结论.
解答 证明:(1)作EG⊥BF,交BF延长线于G,如图所示: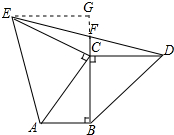
则∠CGE=∠ABC=90°,
∵∠ACE=90°,
∴∠ACB+∠ECG=90°,
∵∠ACB+∠BAC=90°,
∴∠ECG=∠BAC,
在△ABC和△CGE中,
$\left\{\begin{array}{l}{∠ECG=∠BAC}\\{∠CGE=∠ABC}\\{AC=CE}\end{array}\right.$,
∴△ABC≌△CGE(AAS),
∴BC=EG,
∵BC=CD,
∴EG=CD,
∵∠BCD=90°,
∴∠DCF=90°=∠EGF,
在△CFD和△GFE中,
$\left\{\begin{array}{l}{∠DCF=∠EGF}\\{∠CFD=∠GFE}\\{CD=EG}\end{array}\right.$,
∴△CFD≌△GFE(AAS),
∴EF=DF;
(2)∵△CFD≌△GFE,
∴S△CFD=S△GFE,
∴S△CFD+S△CFE=S△GFE+S△CFE,
即S△DCE=S△CGE,
∵△ABC≌△CGE,
∴S△ABC=S△CGE,
∴S△ABC=S△DCE.
点评 本题考查了全等三角形的判定与性质、三角形的面积;本题有一定难度,特别是(1)中,需要通过作辅助线两次证明三角形全等才能得出结论.

练习册系列答案
相关题目
 如图,正方形ABCD的边长为4,E为CD边上一点,DE=3,M为AE的中点,过点M作直线分别与AD、BC相交于点P、Q.若PQ=AE,则AP的长是$\frac{25}{8}$或$\frac{7}{8}$.
如图,正方形ABCD的边长为4,E为CD边上一点,DE=3,M为AE的中点,过点M作直线分别与AD、BC相交于点P、Q.若PQ=AE,则AP的长是$\frac{25}{8}$或$\frac{7}{8}$.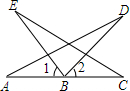 如图,A、B、C在同一条直线上,∠1=∠2,AB=BC,BD=BE.求证:∠D=∠E.
如图,A、B、C在同一条直线上,∠1=∠2,AB=BC,BD=BE.求证:∠D=∠E.
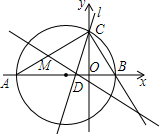 在平面直角坐标系中,△ABC的边AB在x轴上,且OA>OB,以AB为直径的圆与y轴正半轴交于点C,A、B两点的横坐标xA、xB是关于x的方程x2+3x-4=0的两个根.
在平面直角坐标系中,△ABC的边AB在x轴上,且OA>OB,以AB为直径的圆与y轴正半轴交于点C,A、B两点的横坐标xA、xB是关于x的方程x2+3x-4=0的两个根.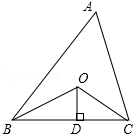 如图所示,已知△ABC的周长是20,OB、OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=3,则△ABC的面积是30.
如图所示,已知△ABC的周长是20,OB、OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=3,则△ABC的面积是30.