题目内容
8.已知(t+58)2=654481,求(t+84)(t+68)的值.分析 由完全平方公式得出t2+116t=654481-582.(t+48)(t+68)=(t2+116t)+48×68,再运用平方差公式计算即可.
解答 解:∵(t+58)2=654481,∴t2+116t+582=654481.
∴t2+116t=654481-582.
∴(t+48)(t+68)
=(t2+116t)+48×68
=654481-582+48×68
=654481-582+(58-10)(58+10)
=654481-582+582-102
=654481-100
=654381.
点评 本题考查了因式分解的运用、完全平方公式、平方差公式;熟练掌握因式分解的运用,熟记完全平方公式是解决问题的关键.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
3.已知△ABC≌△DEF,∠A=∠D=90°,∠B=43°,则∠E的度数是( )
| A. | 43° | B. | 47° | C. | 47°或43° | D. | 43°或57° |
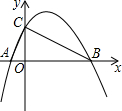 如图,抛物线y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2与x轴交于A、B两点,与y轴交与点C,⊙O′为△ABC的外接圆.
如图,抛物线y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2与x轴交于A、B两点,与y轴交与点C,⊙O′为△ABC的外接圆.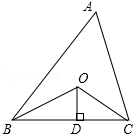 如图所示,已知△ABC的周长是20,OB、OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=3,则△ABC的面积是30.
如图所示,已知△ABC的周长是20,OB、OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=3,则△ABC的面积是30.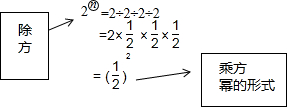 概念学习
概念学习