题目内容
20.已知二次函数y=ax2+bx+c.(1)若a=1,b=-1,c=-2,求此抛物线与坐标轴的交点坐标;
(2)若a=1,b=-4m,c=1-2m,当-1<x<1时,抛物线与x轴有一个公共点,求m的取值范围.
分析 (1)将a、b、c的值代入y=ax2+bx+c得y=x2-x-2,解方程x2-x-2=0得抛物线与x轴的交点的坐标,当x=0时求出对应dey的值,即可得抛物线与y轴的交点的坐标.
(2)列出不等式组,即可解决问题.
解答 解:(1)由题意抛物线解析式为y=x2-x-2,
令x=0则y=-2,令y=0则x2-x-2=0,解得x=2或-1,
∴此抛物线与y轴的交点坐标为(0,-2),与x轴的交点坐标为(2,0),(-1,0).
(2)∵抛物线y=x2-4mx+1-2m,当-1<x<1时,抛物线与x轴有一个公共点,
∴$\left\{\begin{array}{l}{1+4m+1-2m>0}\\{1-4m+1-2m<0}\end{array}\right.$或$\left\{\begin{array}{l}{1+4m+1-2m<0}\\{1-4m+1-2m>0}\end{array}\right.$
解得m>$\frac{1}{3}$或m<-1.
点评 本题考查抛物线与x轴交点问题,解题的关键是熟练掌握求抛物线与坐标轴的交点坐标,学会根据图象,利用不等式组解决问题,属于中考常考题型.

练习册系列答案
相关题目
10.下列是二元一次方程的是( )
| A. | n2+m=5 | B. | 3(x+y)=7(x-y)+10 | C. | 2xy=8 | D. | x-y=2z |
11.在比例尺为1:8000的某市区地图上,康平路长约为25厘米,则它的实际长度约为( )
| A. | 320米 | B. | 320厘米 | C. | 2000厘米 | D. | 2000米 |
12.当字母x分别取下面两个所给数值时,代数式x$+\frac{1}{x}$的值不变的是( )
| A. | $\frac{1}{2}$或-2 | B. | $\frac{1}{2}$或3 | C. | $\frac{1}{3}$或3 | D. | $\frac{1}{3}$或2 |
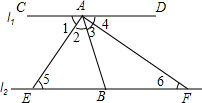 如图,已知直线l1∥直线l2,AE为∠CAB的角平分线,AF为∠DAB的角平分线,试说明:EB=BF.
如图,已知直线l1∥直线l2,AE为∠CAB的角平分线,AF为∠DAB的角平分线,试说明:EB=BF.