题目内容
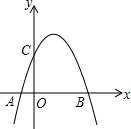 如图,抛物线y=-
如图,抛物线y=-| 1 |
| 2 |
(1)求此抛物线的解析式;
(2)判断△ABC的形状.
考点:抛物线与x轴的交点
专题:
分析:(1)把B(4,0),C(0,2)坐标代入抛物线解析式求出b和c的值即可;
(2)△ABC的形状是直角三角形,由抛物线的解析式可知道A的坐标,所以AB的长可知,再根据勾股定理的逆定理即可判定三角形ACB的形状.
(2)△ABC的形状是直角三角形,由抛物线的解析式可知道A的坐标,所以AB的长可知,再根据勾股定理的逆定理即可判定三角形ACB的形状.
解答:解:(1)∵抛物线y=-
x2+bx+c过B(4,0),C(0,2).
∴
,
解得:
,
∴抛物线的解析式y=-
x2+
x+2;
(2)△ABC的形状是直角三角形,理由如下:
设y=0,则y=-
x2+
x+2=0,
解得:x=-1或4,
∴A的坐标为(-1,0)
∴OA=1,
∴AC=
,AB=5,
∵AC=
,
∴AB2=AC2+BC2=25,
∴△ABC的形状是直角三角形.
| 1 |
| 2 |
∴
|
解得:
|
∴抛物线的解析式y=-
| 1 |
| 2 |
| 3 |
| 2 |
(2)△ABC的形状是直角三角形,理由如下:
设y=0,则y=-
| 1 |
| 2 |
| 3 |
| 2 |
解得:x=-1或4,
∴A的坐标为(-1,0)
∴OA=1,
∴AC=
| 5 |
∵AC=
| 20 |
∴AB2=AC2+BC2=25,
∴△ABC的形状是直角三角形.
点评:本题考查了待定系数法求二次函数解析式,勾股定理以及其逆定理的运用,解题的关键是由抛物线的解析式求出A的坐标.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
 如图,以矩形ABCD的顶点C为圆心作⊙C,⊙C分别交AB、CD于P、Q两点,当CB=2,CQ=4,CD=7时,阴影部分的面积为
如图,以矩形ABCD的顶点C为圆心作⊙C,⊙C分别交AB、CD于P、Q两点,当CB=2,CQ=4,CD=7时,阴影部分的面积为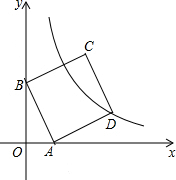 如图,在平面直角坐标系中,直线y=-3x+3与x轴、y轴分别交于A、B两点,以AB为边在第一象限内作正方形ABCD,点D在反比例函数y=
如图,在平面直角坐标系中,直线y=-3x+3与x轴、y轴分别交于A、B两点,以AB为边在第一象限内作正方形ABCD,点D在反比例函数y=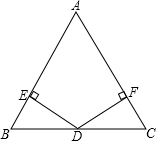 如图:已知在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E、F.
如图:已知在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E、F. Ⅰ.解不等式组5-x<2x-1≤9,并把解集在数轴上表示出来.
Ⅰ.解不等式组5-x<2x-1≤9,并把解集在数轴上表示出来. 如图,A、B、C和D、E、F分别在同一直线上,∠1=∠2,∠C=∠F,求证:∠A=∠D.
如图,A、B、C和D、E、F分别在同一直线上,∠1=∠2,∠C=∠F,求证:∠A=∠D.