题目内容
 如图,A、B、C和D、E、F分别在同一直线上,∠1=∠2,∠C=∠F,求证:∠A=∠D.
如图,A、B、C和D、E、F分别在同一直线上,∠1=∠2,∠C=∠F,求证:∠A=∠D.考点:平行线的判定与性质
专题:推理填空题
分析:根据∠1=∠2,∠2=∠3可知∠1=∠3,证得BF∥CE,从而得出∠4=∠C,又已知∠C=∠F,则可证得∠4=∠F,所以DF∥AC,根据两直线平行内错角相等就可以证出.
解答:证明:∵∠1=∠2,∠2=∠3,
∴∠1=∠3,
∴BF∥CE(同位角相等,两直线平行),
∴∠4=∠C(两直线平行,同位角相等),
∵∠C=∠F,
∴∠4=∠F,
∴DF∥AC(内错角相等,两直线平行),
∴∠A=∠D(两直线平行,内错角相等).
∴∠1=∠3,
∴BF∥CE(同位角相等,两直线平行),
∴∠4=∠C(两直线平行,同位角相等),
∵∠C=∠F,
∴∠4=∠F,
∴DF∥AC(内错角相等,两直线平行),
∴∠A=∠D(两直线平行,内错角相等).
点评:本题考查了平行线的性质和判定以及对顶角的性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知x1,x2是关于x的一元二次方程x2-2x-a=0的两个实数根,且x12+x22+3x1x2=5,则a的值是( )
| A、2 | B、-2 | C、1 | D、-1 |
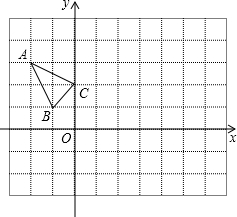 △ABC在平面直角坐标系xOy中的位置如图所示,点A的坐标为(-2,3),点B的坐标为(-1,1),点C的坐标为(0,2).
△ABC在平面直角坐标系xOy中的位置如图所示,点A的坐标为(-2,3),点B的坐标为(-1,1),点C的坐标为(0,2).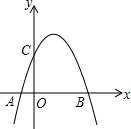 如图,抛物线y=-
如图,抛物线y=-