题目内容
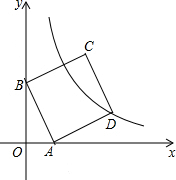 如图,在平面直角坐标系中,直线y=-3x+3与x轴、y轴分别交于A、B两点,以AB为边在第一象限内作正方形ABCD,点D在反比例函数y=
如图,在平面直角坐标系中,直线y=-3x+3与x轴、y轴分别交于A、B两点,以AB为边在第一象限内作正方形ABCD,点D在反比例函数y=| k |
| x |
(1)求k的值;
(2)若将正方形沿x轴负方向平移m个单位长度后,点C恰好落在该反比例函数的图象上,则m的值是多少?
考点:反比例函数综合题
专题:
分析:(1)作DF⊥x轴于点F,先求出A、B两点的坐标,故可得出OB=3,OA=1,再根据AAS定理得出△OAB≌△FDA可得出OF的长,进而得出D点坐标,把D点坐标代入反比例函数的解析式求出k的值即可;
(2)作CE⊥y轴,交反比例函数的图象于点G,同(1)可得△OAB≌△EBC,OB=BC,OA=BE,故可得出C点坐标,把C点纵坐标代入(1)中的反比例函数解析式即可得出G点坐标,进而得出结论.
(2)作CE⊥y轴,交反比例函数的图象于点G,同(1)可得△OAB≌△EBC,OB=BC,OA=BE,故可得出C点坐标,把C点纵坐标代入(1)中的反比例函数解析式即可得出G点坐标,进而得出结论.
解答: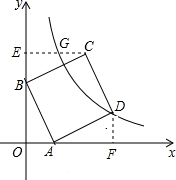 解:(1)作DF⊥x轴于点F.
解:(1)作DF⊥x轴于点F.
在y=-3x+3中,令x=0,则y=3,即B(0,3),
令y=0,则x=1,即A(1,0),则OB=3,OA=1,
∵∠BAD=90°,
∴∠BAO+∠DAF=90°,
∵Rt△ABO中,∠BAO+∠DAF=90°,
∴∠DAF=∠OBA,
在△OAB与△FDA中,
,
∴△OAB≌△FDA(AAS),
∴AF=OB=3,DF=OA=1,
∴OF=4,
∴D(4,1),
∵点D在反比例函数y=
(k≠0)的图象上,
∴1=
,解得k=4;
(2)作CE⊥y轴,交反比例函数的图象于点G,
∵同(1)可得△OAB≌△EBC,
∴OB=BC=3,OA=BE=1,
∴OE=4,C(3,4),
∵点C的纵坐标是4,
∴G(1,4),
∴CG=2,即m=2.
 解:(1)作DF⊥x轴于点F.
解:(1)作DF⊥x轴于点F.在y=-3x+3中,令x=0,则y=3,即B(0,3),
令y=0,则x=1,即A(1,0),则OB=3,OA=1,
∵∠BAD=90°,
∴∠BAO+∠DAF=90°,
∵Rt△ABO中,∠BAO+∠DAF=90°,
∴∠DAF=∠OBA,
在△OAB与△FDA中,
|
∴△OAB≌△FDA(AAS),
∴AF=OB=3,DF=OA=1,
∴OF=4,
∴D(4,1),
∵点D在反比例函数y=
| k |
| x |
∴1=
| k |
| 4 |
(2)作CE⊥y轴,交反比例函数的图象于点G,
∵同(1)可得△OAB≌△EBC,
∴OB=BC=3,OA=BE=1,
∴OE=4,C(3,4),
∵点C的纵坐标是4,
∴G(1,4),
∴CG=2,即m=2.
点评:本题考查的是反比例函数综合题,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
相关题目
4的算术平方根是( )
| A、2 |
| B、-2 |
| C、±2 |
| D、a2+a2=a4 |
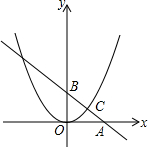 如图,直线y=kx+b交坐标轴于A、B两点,交抛物线y=ax2于点C(4,3),且C是线段AB的中点,抛物线上另有位于第一象限内的一点P,过P的直线y=k′x+b′交坐标轴于D、E两点,且P恰好是线段DE的中点,若△AOB∽△DOE,则P点的坐标是
如图,直线y=kx+b交坐标轴于A、B两点,交抛物线y=ax2于点C(4,3),且C是线段AB的中点,抛物线上另有位于第一象限内的一点P,过P的直线y=k′x+b′交坐标轴于D、E两点,且P恰好是线段DE的中点,若△AOB∽△DOE,则P点的坐标是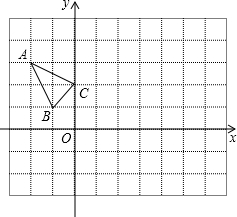 △ABC在平面直角坐标系xOy中的位置如图所示,点A的坐标为(-2,3),点B的坐标为(-1,1),点C的坐标为(0,2).
△ABC在平面直角坐标系xOy中的位置如图所示,点A的坐标为(-2,3),点B的坐标为(-1,1),点C的坐标为(0,2). 阅读材料:
阅读材料:
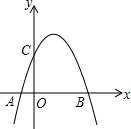 如图,抛物线y=-
如图,抛物线y=-